基本概念
 切線三角形
切線三角形 切線三角形
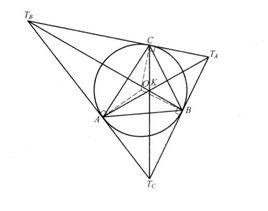
切線三角形過△ABC的各個頂點作其外接圓的切線,三切線兩兩相交於 , 是△ABC的 切線三角形(Tangential Triangle)。它是△ABC外心O的反垂足三角形,也是△ABC的共軛重心的反切瓦三角形,如圖1。
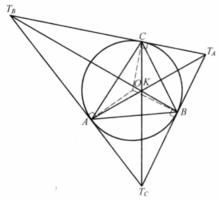 圖1
圖1相關性質及定理
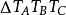 切線三角形
切線三角形① △ABC中的共軛重心就是 的熱爾崗點。
② 切線三角形是外接圓的極三角形。
③ 切線三角形的三線坐標矩陣是
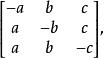 切線三角形
切線三角形其各邊的邊長是
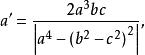 切線三角形
切線三角形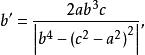 切線三角形
切線三角形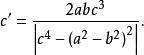 切線三角形
切線三角形其面積是
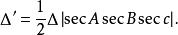 切線三角形
切線三角形④ 表1中列出了切線三角形內的特徵點與原三角形內特徵點的對應關係。
| 切線三角形中的特徵點 | 原△ABC內的特徵點 |
重心 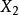 切線三角形 切線三角形 | 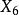 切線三角形 切線三角形 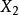 切線三角形 切線三角形 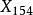 切線三角形 切線三角形 |
外心 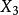 切線三角形 切線三角形 | 切線三角形的外心 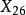 切線三角形 切線三角形 |
垂心 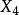 切線三角形 切線三角形 | 垂足三角形的本徵中心 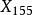 切線三角形 切線三角形 |
九點圓圓心 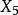 切線三角形 切線三角形 | 切線三角形中的 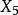 切線三角形 切線三角形 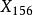 切線三角形 切線三角形 |
共軛重心 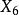 切線三角形 切線三角形 | 切線三角形中的 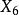 切線三角形 切線三角形 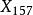 切線三角形 切線三角形 |
歐拉無窮遠點 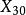 切線三角形 切線三角形 | 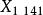 切線三角形 切線三角形 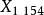 切線三角形 切線三角形 |
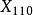 切線三角形 切線三角形 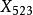 切線三角形 切線三角形 | 拿破崙交叉差 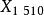 切線三角形 切線三角形 |
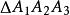 切線三角形
切線三角形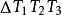 切線三角形
切線三角形 切線三角形
切線三角形 切線三角形
切線三角形⑤ 給定 和它的切線三角形 ,兩三角形的三條邊兩兩相交於 ,則 共線,如圖2 。
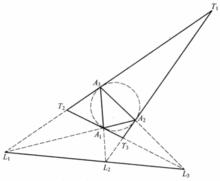 圖2(a)
圖2(a)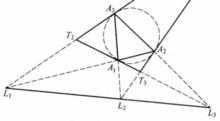 圖2(b) (a)的放大圖
圖2(b) (a)的放大圖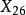 切線三角形
切線三角形⑥ 切線三角形的外接圓稱為切線圓,它的圓心是
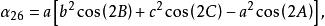 切線三角形
切線三角形其半徑是
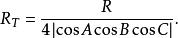 切線三角形
切線三角形⑦ 下面介紹一個有關切線三角形的定理:
設△ABC的切線三角形是△A'B'C',設A",B",C"是在△ABC外接圓上的任意三點,則有
定理1(斯坦巴特(Stein bart)) 若且唯若直線AA”,BB"和CC"共點,或AA”∩BC,BB"∩CA,CC"∩AB共線時,A'A",B'B"和C'C"共點,如圖3 。
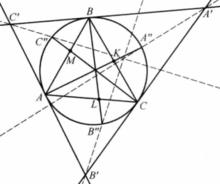 圖3
圖3