作者介紹
克萊姆基本介紹
假若有n個未知數，n個方程組成的方程組：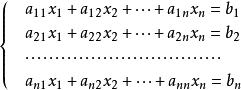
克拉默法則克萊姆法則不僅僅適用於實數域，它在任何域上面都可以成立。
使用克萊姆法則求線性方程組的解的算法時間複雜度依賴於矩陣行列式的算法複雜度O(f(n))，其複雜度為O(n·fn)，一般沒有計算價值，複雜度太高。
當b1,b2,...,bn不全為0時，方程組為非齊次性方程組。
係數矩陣A非奇異時，或者說行列式|A|≠0時，方程組有唯一的解；
係數矩陣A奇異時，或者說行列式|A|=0時，方程組有無數個解或無解。
當b1=b2=...=bn=0時，方程組為齊次性方程組。
若係數矩陣A非奇異時，則方程組有唯一的解，其所有分量均為0，我們通常稱這個解為平凡解。
若齊次線性方程組有非零解，係數矩陣必然奇異，或者說對應的係數行列式必為0。
其實萊布尼茲〔1693〕，以及馬克勞林〔1748〕亦知道這個法則，但他們的記法不如克萊姆。
內容要點
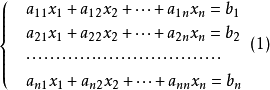克拉默法則從三元線性方程組的解的討論出發，對更一般的線性方程組進行探討。
在引入克萊姆法則之前，先引入有關n元線性方程組的概念。
含有n個未知數的線性方程組稱為n元線性方程組。當其右端的常數項不全為零時，線性方程組⑴稱為非齊次線性方程組，當全為零時，線性方程組⑵稱為齊次線性方程組，即：
定理
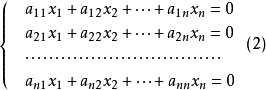克拉默法則一般來說，用克萊姆法則求線性方程組的解時，計算量是比較大的.對具體的數字線性方程組，當未知數較多時往往可用計算機來求解。用計算機求解線性方程組目前已經有了一整套成熟的方法。
克拉默法則在一定條件下給出了線性方程組解的存在性、唯一性，與其在計算方面的作用相比，克萊姆法則更具有重大的理論價值。
法則總結
1：克萊姆法則的重要理論價值：研究了方程組的係數與方程組解的存在性與唯一性關係;
2：套用克萊姆法則判斷具有N個方程、N個未知數的線性方程組的解:
（1）：當方程組的係數行列式不等於零時，則方程組有解，且具有唯一的解；
（2）：如果方程組無解或者有兩個不同的解，那么方程組的係數行列式必定等於零；
3：克萊姆法則的局限性：
（1）：當方程組的方程個數與未知數的個數不一致時，或者當方程組係數的行列式等於零時，克萊姆法則失
效。
（2）：運算量較大，求解一個N階線性方程組要計算N+1個N階行列式。
技術套用
克拉默法則克萊姆法則在解決微分幾何方面十分有用。
先考慮兩條等式和。因為u和v都是沒相關的變數，我們可定義和。
找出一條等式適合是克萊姆法則的簡單套用。
首先，我們要計算F、G、x和y的導數：
然後用兩個雅可比矩陣來表示的方程：
用類似的方法就可以找到。
