佩特里網論

佩特里網論是網論分支之一，又稱特殊網論。

佩特里網論

正文

網論分支之一，又稱特殊網論。研究如何將佩特里網模擬系統以及佩特里網的分析技術，適用於無中央控制的異步並發系統的動態定性研究。佩特里網論是聯邦德國C.A.佩特里於20世紀60年代初創建的。佩特里網已在西歐、北歐和美國獲得廣泛套用。
兩種表示法　佩特里網有圖表示和數學表示兩種表示法。
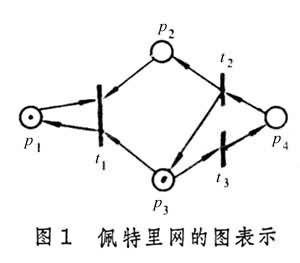
① 圖表示： 佩特里網是由圓圈和短線兩類節點構成的網狀結構（圖1）。圓圈表示地點或條件，短線表示變遷或事件。連線圓圈和短線的有向弧稱為流關係，圓圈中的黑點叫作碼子，標誌著網中的信息，信息的流動即用碼子的位置和數量的變化模擬。碼子在網中的分布構成網的標識，又稱狀態。上述要素所構成之網狀結構滿足以下五個條件才是佩特里網：(a)至少有一個節點；(b)每個有向弧的起止點必須是一個圓圈和一條短線，兩條有向弧的起止點不能完全相同；(c)每個節點至少必須是一條有向弧的起點或終點；(d)每個地點都有固定的容量,即最多能容納的碼子個數,容量可以是無窮的(ω)；(e)每個網都有一個初始標識。

佩特里網論

為敘述方便起見，可以對節點起名字（如p1,p2,t3等），但這些名字不是定義的組成部分。
② 數學表示:將圖示中的各要素表示為數學對象。P,T分別為圓圈和短線的集合；F為流關係；K,μ:P→N +ω分別為容量函式和標識。五元組(P，T，F，K，μ)成為佩特里網的條件可以形式地定義為

式中φ為空集；N +ω為自然數（包括零）上無窮之集合；dom F和cod F分別為F 的定義域和值域;P×T及T×P均為笛卡兒積。
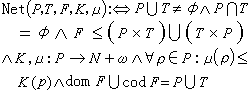
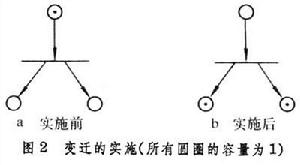
變遷的實施規則　變遷的實施改變碼子的位置和數量，標識的變化記錄著系統的動態性質。
若存在有向弧從地點p指向變遷t，則p即是t的輸入地點；反之,若有向弧從t指向p,則p是t的輸出地點。若在標識μ之下,t的每個輸入地點都至少有一個碼子，且t的每個輸出地點中的碼子數都比其容量至少小1，那么t在μ之下是具備條件的。凡具備條件的變遷均可實施。實施辦法是先從t的輸入地點各拿掉一個碼子，再在t的輸出地點各放一個碼子，如此得到的新標識稱為μ′(圖2)。

佩特里網論

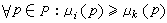分析技術　從初始標識μ出發,通過變遷之實施獲得新的標識，所有這些標識之集合稱為可到達狀態集，記為R(μ)。構造佩特里網的可到達狀態樹是研究R(μ)的通用分析技術。構造的步驟是：①以μ為根，記作μ0；μ0和一切標識均表示為矢量(n1,n2,…),其中ni是在該標識下地點Pi中的碼子個數。②若μi是已構造的樹的葉節點,則分四種情況處理：(a)若在ui之下ti1，ti2，…,tij均具備條件，則μi有j個子分枝,分別標以ti1，ti2，…，tij,相應的子節點依次為在μi之下實施變遷ti1，ti2,…，tij所得之新標識。(b)若在從μ0到μi的道路上存在節點μk, 使得,且p∈P:μi(p)＞μk(p)，那么對所有p，只要μi(p)＞μk(p),就把μi(p)改為ω，這樣從μi獲得新標識μ'i，即以μ'i代替μi作為節點。(c)若上述μk使凬p∈P:μi(p)＝μk(p)，那么μi即為最終之葉節點。(d)在μi之下任何變遷均不具備條件,這時μi為最終之葉節點。下面是圖1所示佩特里網的可到達樹

分析可到達樹可以獲得系統的動態性質。例如是否可能達到指定的狀態，是否有永不能實施的變遷等。這些都是佩特里網論分析研究的問題。
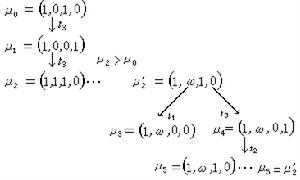
擴充網和受限網　擴充網具有較強的模擬力，限受網則易於分析，有較強的決策力。一種有意義的擴充網是約束弧網，這種網與圖靈機有相同的模擬力。
簡單網和單純網是兩種重要的受限網。前者要求任意兩個節點不能有完全相同的輸入和輸出；後者則要求若有向弧(x，y)∈F……,則(y，x)唘F。圖1中的網是簡單的，但不單純。
套用　變遷的實施只決定於變遷本身的輸入輸出，所以佩特里網特別適用於模擬無中央控制的異步並發系統的動態性質。佩特里網已成功地用於分析作業系統和計算機系統結構的容錯性能。佩特里網的缺點是節點過多，通用網論中的網射是克服這一缺點的有力工具。

配圖

相關連線