簡介
更一般的是在每個坐標軸方向上的有單獨縮放因子的 縮放；特殊情況是 方向縮放（在一個方向上）。形狀可能變化，比如矩形可能變成不同形狀的矩形，還可能變成平行四邊形（保持在平行於軸的線之間的角度，但不保持所有的角度）。
矩陣表示
縮放可以表示為縮放矩陣。要用一個向量 v= ( v, v, v)縮放一個物體，每個點 p= ( p, p, p)都需要乘以縮放矩陣：
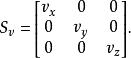位似變換如下所示，這個乘法將給出預期的結果：
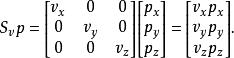位似變換這種縮放按在縮放因子中間的一個因子改變物體的直徑，那在在兩個縮放因子的最小和最大乘積之間的一個因子改變它的面積，按所有三個縮放因子的乘積改變它的體積。
在最一般意義上的縮放是使用可對角化矩陣的任何仿射變換。它包括縮放的三個方向不垂直的情況。它還包括一個或多個縮放因子等於零的情況（投影），和一個或多個負縮放因子的情況 。
齊次坐標
使用齊次坐標經常是更加有用的，因為3次元的平移（仿射變換）不能用3 × 3矩陣完成。要按一個向量 v= ( v, v, v)縮放一個物體，所有的齊次向量 p= ( p, p, p, 1)都需要乘以縮放矩陣 ：
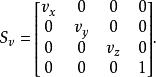位似變換如下所示，這個乘法給出預期的結果：
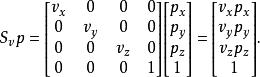位似變換縮放是均勻的，若且唯若縮放因子是相等的。如果除了一個因子之外所有縮放因子都是1我們得到方向縮放。
因為齊次坐標的最後成員可以看作其他三個成員的分母，使用公共因子 s的縮放可以使用如下縮放矩陣完成：
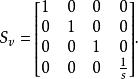位似變換對於每個齊次向量 p=（ p, p, p, 1），我們有
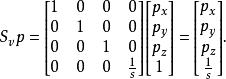位似變換它將均質於
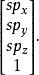位似變換圖形描述
給定位似中心和位似比，原圖形經位似變換能得到兩個新的圖形，他們都和原圖形位似。分別描述如下：
（1）依次有一個點光源，一個不透明幾何圖形，一張幕布。
該圖形在幕布上的投影就是一個位似圖形；
（2）依次有一個發光的幾何圖形，破了一張小孔的幕布以及另一張幕布。
該圖形在第二張幕布上的小孔成像即是另一個位似圖形。
注意：此描述只限於平面上的幾何圖形；
另外，點和圖形不能在同一個平面上，
且（1）中幕布與該圖形所在平面平行，（2）中圖形所在平面與第二張幕布平行 。
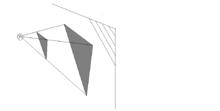圖1
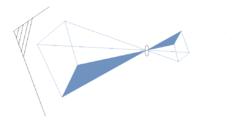圖2