定義
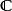魏爾斯特拉斯橢圓函式
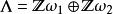魏爾斯特拉斯橢圓函式
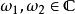魏爾斯特拉斯橢圓函式
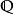魏爾斯特拉斯橢圓函式固定 中的格 （ 在 上線性無關 ），對應的魏爾斯特拉斯橢圓函式定義是
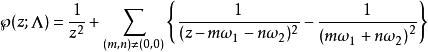魏爾斯特拉斯橢圓函式。
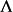魏爾斯特拉斯橢圓函式
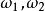魏爾斯特拉斯橢圓函式 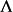魏爾斯特拉斯橢圓函式顯然右式只與格 相關，無關於基 之選取。 的元素也稱作周期。
魏爾斯特拉斯橢圓函式
魏爾斯特拉斯橢圓函式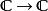
魏爾斯特拉斯橢圓函式
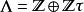魏爾斯特拉斯橢圓函式另一方面，格 在取適當的全純同態 後可表成 ，其中 屬於上半平面。對於這種形式的格，
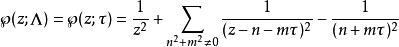魏爾斯特拉斯橢圓函式。
反之，由此亦可導出對一般的格之公式
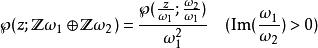魏爾斯特拉斯橢圓函式
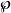魏爾斯特拉斯橢圓函式在數值計算方面， 可以由Θ函式快速地計算，方程是
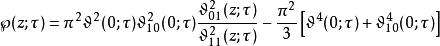魏爾斯特拉斯橢圓函式 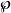魏爾斯特拉斯橢圓函式在周期格中的每個點， 有二階極點。
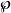魏爾斯特拉斯橢圓函式是偶函式。
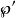魏爾斯特拉斯橢圓函式復導函式 是奇函式。
加法定理
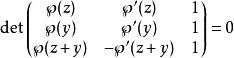魏爾斯特拉斯橢圓函式
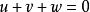魏爾斯特拉斯橢圓函式假設 ，上式有一個較對稱的版本
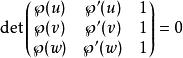魏爾斯特拉斯橢圓函式此外
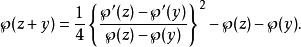魏爾斯特拉斯橢圓函式
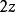魏爾斯特拉斯橢圓函式魏爾斯特拉斯橢圓函式滿足複製公式：若 不是周期，則
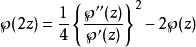魏爾斯特拉斯橢圓函式微分方程與積分方程
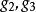魏爾斯特拉斯橢圓函式 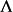魏爾斯特拉斯橢圓函式定義 （依賴於 ）為
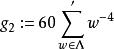魏爾斯特拉斯橢圓函式
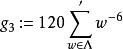魏爾斯特拉斯橢圓函式
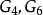魏爾斯特拉斯橢圓函式
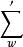魏爾斯特拉斯橢圓函式
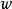魏爾斯特拉斯橢圓函式 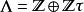魏爾斯特拉斯橢圓函式求和符號 意謂取遍所有非零的 。當 時，它們可由艾森斯坦級數表示。
則魏爾斯特拉斯橢圓函式滿足微分方程
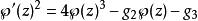魏爾斯特拉斯橢圓函式
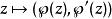魏爾斯特拉斯橢圓函式
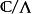魏爾斯特拉斯橢圓函式
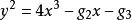魏爾斯特拉斯橢圓函式故給出了從復環面映至三次復射影曲線的全純映射；可證明這是同構。
另一方面，將上式同除以{\displaystyle \wp '}，積分後可得
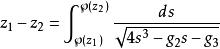魏爾斯特拉斯橢圓函式
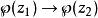魏爾斯特拉斯橢圓函式 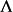魏爾斯特拉斯橢圓函式 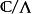魏爾斯特拉斯橢圓函式右側是複平面上的路徑積分，對不同的路徑，其積分值僅差一個的元素；所以左式應在復環面 中考慮。在此意義下，魏爾斯特拉斯橢圓函式是某類橢圓積分之逆 。
模判別式
魏爾斯特拉斯橢圓函式續用上節符號， 模判別式定義為下述函式
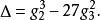魏爾斯特拉斯橢圓函式視為周期格的函式，這是權 12 之模形式。模判別式也可以用戴德金η函式表示。
