零導數定理

簡介

零導數定理是可微函式為常值函式的充分必要條件。

若一元函式f在區間I上連續，在I的內部可微，則f為I上為常值函式的充分必要條件是f'=0。

條件

零導數定理的條件可以減弱為：在I上連續，除可數個點外存在等於零的右導數。

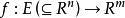零導數定理

一般地，對向量值函式。

若E是連通開集，則f為常值的充要條件是：對任意x∈E，有Df(x)=0，即對任意i=1,2,...,m，j=1,2,...,n，Df(x)=0。特別地，當m=1時，條件成為grad f=0。

定義域

零導數定理中，f的定義域的連通性是必不可少的。

例如：設m=n=1，E=(-2,-1)U(0,1)，且x∈(-2,-1)時，f(x)=1，x∈(0,1)時，f(x)=0，則f'=0，但f非常值。

R 和R 換成任意賦范線性空間時這個定理仍成立。