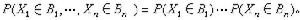金屬光學
正文
研究金屬的光學性質及其與金屬物質結構關係的學科。金屬最顯著的光學特性是反射高,吸收強,要薄到300~400埃才開始透光。這同金屬具有良好的導電性有關。發展簡史 金屬光學的發展歷史可追溯到19世紀中葉提倡光的彈性以太理論時期,透明媒質的菲涅耳公式(見光在分界面上的折射和反射)那時已建立起來。人們開始注意研究金屬的反射性能,並測量了它的折射率和吸收係數。但是金屬光學的重大進展是在麥克斯韋光的電磁理論問世之後。特別是20世紀初,P.K.L.德魯德將經典電子論套用於金屬媒質,使金屬的光學常數同其自由電子參量建立起關係。但理論和實驗不盡一致。此後的研究工作主要在實驗方面。例如,在高真空中製備樣品,提高光學量的測量準確度,進行低溫測量以觀測溫度效應等等。隨著固體物理學的發展,金屬光學到50年代便完全納入固體物理學的研究領域,以量子理論為理論基礎了。但由於歷史原因,一些光學教本現仍辟有“金屬光學”章節,主要討論金屬的巨觀光學性質及其經典色散理論。本條介紹亦限於此,其他可參見固體的能帶等。
學科內容 下面主要討論金屬的光學性質和根據經典電子理論(見金屬電子論)來分析金屬的光學性質。
吸收媒質的復折射率 光波是電磁波,在金屬中傳播時會因焦耳熱損耗而衰減,造成金屬媒質對光的吸收。吸收媒質中的單色平面波通常可表成
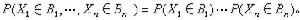
金屬對光的反射 根據菲涅耳公式,光在界面正入射時空氣-金屬界面的振幅反射係數為
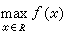
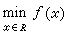
斜入射時,同樣可根據菲涅耳公式來計算有關各量。這時s分量(振動垂直於入射面)和p分量(振動平行於入射面)的反射相變不等,因而線偏振光經金屬界面反射一般成為橢圓偏振光。測出此橢圓的方位角和軸長之比,可通過相應公式計算出n和ⅹ。這是測定金屬光學常數的一種重要方法。
下表列出一些典型金屬的n、ⅹ 和R值(λ0=5893埃)。
 金屬光學
金屬光學
 稱為吸收係數。ⅹ=1時,k≈2.5×105厘米-1(設λ0≈0.5微米)。這個量級的k值代表強吸收。距離
稱為吸收係數。ⅹ=1時,k≈2.5×105厘米-1(設λ0≈0.5微米)。這個量級的k值代表強吸收。距離 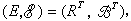 稱為透入深度。取上列k值時,d≈4×10-6厘米=400埃。所以,在金屬的強吸收區,光波僅能進入其界面內極薄一層地區。按照交流電輸送技術用語,人們亦稱此為趨膚效應,d/2則稱為趨膚深度。
稱為透入深度。取上列k值時,d≈4×10-6厘米=400埃。所以,在金屬的強吸收區,光波僅能進入其界面內極薄一層地區。按照交流電輸送技術用語,人們亦稱此為趨膚效應,d/2則稱為趨膚深度。 n、ⅹ的色散和溫度效應 金屬的光學常數n、ⅹ隨波長改變,即二者有色散。作為示例,圖1給出0.2~10.0微米波段Ag的n、ⅹ色散曲線。大體上說,從紅外往長波,金屬的n、ⅹ 隨λ0單調增大。數量級可從10增加到102,反射自然很高;從可見往短波,到200nm以下,曲線n(λ0)和ⅹ(λ0)具有一定結構。按照固體理論,紅外區以遠是金屬中傳導電子(經典自由電子)同光相互作用起主導的波段,即色散機制來自導帶電子的帶內運動;而紫外一端,光子能量較高,金屬電子的帶間躍遷開始參與作用。
 金屬光學
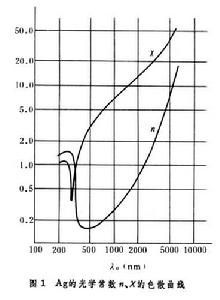
金屬光學金屬光學常數n、ⅹ又是溫度T的函式。圖2 給出Na的吸收(Na)對溫度的依賴關係。在自由電子吸收區(長波),Na隨溫度T增大;在帶間躍遷吸收區(短波),溫度效應可因吸收帶而異。
 金屬光學
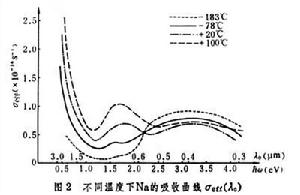
金屬光學根據麥克斯韋方程組,在單色場下可引進一個復介電常數
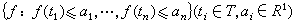
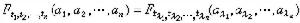 ,
,
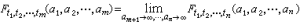 , (1)
, (1)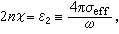 (2)
(2)
在靜電場下,金屬中的自由電子獲得附加定向速度,形成傳導電流。嚴格計算需藉助統計理論。簡單處理可採用模型電子,從其運動方程
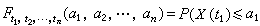 導出電導率
導出電導率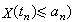 式中N是單位體積內自由電子數;e是電子電荷;m是電子質量(固體物理中換作傳導電子的有效質量m*);τ是弛豫時間,粗略地講就是自由電子在運動中經受碰撞相隔的平均時間,其典型數量級是10-14,秒。
式中N是單位體積內自由電子數;e是電子電荷;m是電子質量(固體物理中換作傳導電子的有效質量m*);τ是弛豫時間,粗略地講就是自由電子在運動中經受碰撞相隔的平均時間,其典型數量級是10-14,秒。 在時諧電場下,金屬的電導率
 (3)
(3)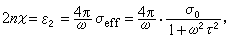 (4)
(4)
式(3)、(4)描寫金屬自由電子弛豫效應所導致的n、ⅹ色散。
當ωτ
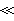 1時,Na=N0,ε1=1+4πα0
1時,Na=N0,ε1=1+4πα0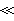 ε2,這時可得到經典趨膚深度
ε2,這時可得到經典趨膚深度 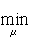
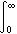
稱魯賓斯-哈根(Rubens-Hagen)關係。
當ωτ
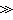 1時,弛豫效應強烈,由式(3)可得到
1時,弛豫效應強烈,由式(3)可得到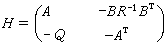
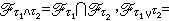 其中a=1+4πα0,
其中a=1+4πα0,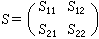 實驗證明n2-ⅹ2和
實驗證明n2-ⅹ2和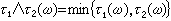 成線性關係,並由此求得α0和N/m。
成線性關係,並由此求得α0和N/m。 弛豫效應很強時,
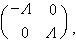 傳導電流和光場的位相差約90°,自由電子的極化作用遠大於吸收,金屬類似介質。如果令τ→∞,則吸收2nⅹ=ε2→0,而
傳導電流和光場的位相差約90°,自由電子的極化作用遠大於吸收,金屬類似介質。如果令τ→∞,則吸收2nⅹ=ε2→0,而 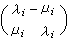
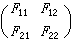 (α0設為零)。這樣,當ω<ωc時,ε1<0,因而n=0,
(α0設為零)。這樣,當ω<ωc時,ε1<0,因而n=0,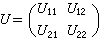 R →1;當ω>ωc時,ε1>0,因而
R →1;當ω>ωc時,ε1>0,因而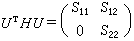 ,ⅹ=0。所以頻率ωc是τ值有限時金屬從高反射過渡到弱吸收的臨界標誌,相應波長就是臨界波長λc。
,ⅹ=0。所以頻率ωc是τ值有限時金屬從高反射過渡到弱吸收的臨界標誌,相應波長就是臨界波長λc。 ω=ωc時,ε1=0。
這正好是無限大理想金屬中電漿振盪的頻率條件。所以金屬的臨界頻率ωc就等於金屬的電漿頻率。反常趨膚效應 電磁場的趨膚深度δf與金屬的電導率
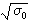 成反比,而N0與溫度T有關。降低金屬溫度T,可減小δf。當δf接近甚至小於金屬中傳導電子的平均自由程l時,就必須考慮電磁場的空間衰減對電子運動的影響。這時通常的歐姆定律j=N0E 和以此為基礎的經典理論均告失效,結果產生反常趨膚效應。這主要是一個高頻和低溫效應,其典型現象是金屬吸收率A 這時與N0(T)無關而為一常數。顯然這時傳導電子在金屬內表面上的散射機理和能量損失決定吸收率A。
成反比,而N0與溫度T有關。降低金屬溫度T,可減小δf。當δf接近甚至小於金屬中傳導電子的平均自由程l時,就必須考慮電磁場的空間衰減對電子運動的影響。這時通常的歐姆定律j=N0E 和以此為基礎的經典理論均告失效,結果產生反常趨膚效應。這主要是一個高頻和低溫效應,其典型現象是金屬吸收率A 這時與N0(T)無關而為一常數。顯然這時傳導電子在金屬內表面上的散射機理和能量損失決定吸收率A。 1940年,由於雷達研究的需要,A.B.皮帕德在測量Sn的高頻低溫電導率時發現了這一效應。隨後有人給出了詳細的理論分析。
參考書目
M.玻恩、E.沃耳夫著,黃樂天等譯:《光學原理》,下冊,科學出版社,北京,1981。(M.Born and E. Wolf,Principles of Optics,5th ed., Pergamon Press, Oxford, 1975.)
F.Abeles,ed.,Optical Properties and Electronic Structure of Metals and Alloys,North-Holland,Amsterdam,1966.