運算元內插
正文
證明運算元有界性的一種數學方法。如果運算元T 是Lp到Lq的有界運算元,即對所有的ƒ∈Lp,有Tƒ∈Lq,且滿足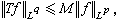
里斯-索林定理 如果線性運算元T 同時是強(p1,q1)和強(p2,q2)型的,其中1≤pj≤∞,1≤qj≤∞(j=1,2),即
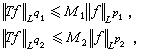
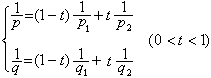 (1)
(1)
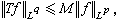
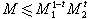 。
。
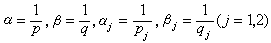 則α1、α 2表示區間【0,1】上的兩點,α在α1,α 2之間,構想β是α 的函式,在α1時取值β1,在α 2時取值β2,問β在α點取什麼值?關係式(1)表明β的值恰好等於在(α1,β1)和(α 2,β2)作線性內插時的線性函式在α 取的值(圖1
則α1、α 2表示區間【0,1】上的兩點,α在α1,α 2之間,構想β是α 的函式,在α1時取值β1,在α 2時取值β2,問β在α點取什麼值?關係式(1)表明β的值恰好等於在(α1,β1)和(α 2,β2)作線性內插時的線性函式在α 取的值(圖1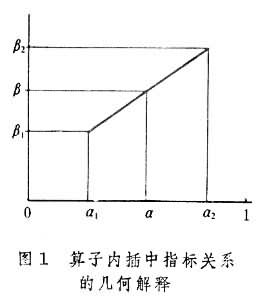 )。這就是運算元內插這個名稱的由來。
)。這就是運算元內插這個名稱的由來。 里斯-索林定理說明,要證明一個線性運算元T是Lp到Lq有界的,只須驗證T同時是L
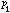 到L
到L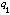 和L
和L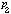 到L
到L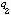 有界的。也就是說,要得到T 是強
有界的。也就是說,要得到T 是強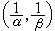 型的,只需驗證T 線上段的兩個端點具有相應的型,即同時是強
型的,只需驗證T 線上段的兩個端點具有相應的型,即同時是強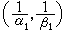 型和強
型和強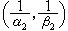 型就可以了。
型就可以了。 下面通過一個典型例子來看如何套用這種運算元內插的方法。
豪斯多夫-楊定理 設弮是ƒ的傅立葉變換,即
 ,
,
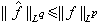 ,
,
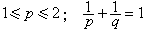 。
。
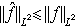 是帕舍伐爾等式的推論。取p2=1,q2=∞,這時顯然有
是帕舍伐爾等式的推論。取p2=1,q2=∞,這時顯然有 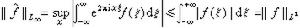 。用里斯-索林定理便得所要證的結果(圖2
。用里斯-索林定理便得所要證的結果(圖2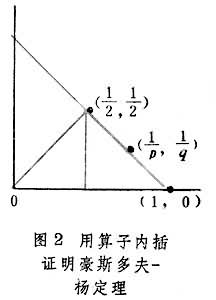 )。如果不用運算元內插,這定理的證明就困難得多。
)。如果不用運算元內插,這定理的證明就困難得多。 里斯-索林定理的條件可以減弱。首先,線性運算元的條件可用次可加性代替,所謂次可加性是指對任意的ƒ,g,皆有
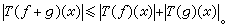
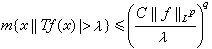
馬欽凱維奇內插定理 如果次可加運算元 T同時是弱(p1,q1)型和弱(p2,q2)型的,即
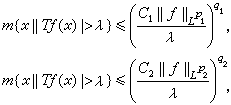
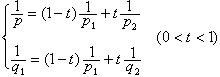
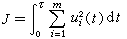
除上述兩個定理外,還有許多其他類型的運算元內插定理。近代的運算元內插理論,已經從Lp空間推廣到其他許多的空間, 例如索伯列夫空間、Hp 空間、別索夫空間等等。
運算元內插的方法不僅在調和分析,還在泛函分析、偏微分方程的理論中有許多套用。
參考書目
E.M.Stein and G.Weiss,lntroduction to Fourier Analysis on Euclidean Spaces, Princeton Univ. Press, Princeton, 1971.
A.Zygmund,Trigonometrical Series,2nd ed., Vol. 1~2,Cambridge Univ.Press, Cambridge, 1959.
