歷史
皮埃爾•德•費馬於1636年發現了這個定理,在一封1640年10月18日的信中他第一次使用了上面的書寫方式。在他的信中費馬還提出a是一個質數的要求。這個要求實際上不存在。
 費馬小定理
費馬小定理 費馬小定理
費馬小定理 費馬小定理
費馬小定理 費馬小定理
費馬小定理與費馬無關的有一個中國猜想。這個猜想是中國數學家提出來的。其內容為如果,而且只有當2p = 2(mod p)成立時p才是一個質數。
假如p是一個質數的話,則2p = 2(mod p)成立(這是費馬小定理的一個特殊情況)是對的。但反過來,假如2p = 2(mod p)成立那么p是一個質數是不成立的(比如341符合上述條件但不是一個質數)。因此整個來說這個猜想是錯誤的。
一般認為中國數學家在費馬前2000年的時候就已經認識中國猜測了。但也有人認為實際上中國猜測是1872年提出的,認為它早就為人所知是出於一個誤解。
證明
一、準備知識:
引理1.剩餘系定理2若a,b,c為任意3個整數,m為正整數,且(m,c)=1,則當ac≡bc(modm)時,有a≡b(modm)
證明:ac≡bc(mod m)可得ac–bc≡0(mod m)可得(a-b)c≡0(mod m)因為(m,c)=1即m,c互質,c可以約去,a–b≡0(mod m)可得a≡b(mod m)
引理2.剩餘系定理5若m為整數且m>1,a,a,a,a,…a[m]為m個整數,若在這m個數中任取2個整數對m不同餘,則這m個整數對m構成完全剩餘系。
證明:構造m的完全剩餘系(0,1,2,…m-1),所有的整數必然這些整數中的1個對模m同餘。取r=0,r=1,r=2,r=3,…r=i-1,1引理3.剩餘系定理7設m是一個整數,且m>1,b是一個整數且(m,b)=1。如果a1,a2,a3,a4,…am是模m的一個完全剩餘系,則ba,ba,ba,ba,…ba[m]也構成模m的一個完全剩餘系。
證明:若存在2個整數ba和ba[j]同餘即ba≡ba[j](mod m),根據引理2則有a≡a[j](mod m)。根據完全剩餘系的定義和引理4(完全剩餘系中任意2個數之間不同餘,易證明)可知這是不可能的,因此不存在2個整數ba和ba[j]同餘。由引理5可知ba,ba,ba,ba,…ba[m]構成模m的一個完全剩餘系。
引理4.同餘定理6如果a,b,c,d是四個整數,且a≡b(mod m),c≡d(mod m),則有ac≡bd(mod m)
證明:由題設得ac≡bc(mod m),bc≡bd(mod m),由模運算的傳遞性可得ac≡bc(mod m)
證明
假如a和b 的 差不能被n整除的話 , 那么假如x>0和x和n的最 大 公約數為1 的 話 , 則x•a與x•b 的 差也不能 被n整除。取A為所有小於p 的 整數的集(A中的數都不能被p整除),B為A中所有元素乘 以a所獲得的 數的 集。任何兩 個A中 的 元素的差都不能被p整除。由此任何兩個B中的元素的差也無法被p整除。由此
1 \cdot 2 \cdot 3 \cdot \dots \cdot (p-1) \equiv (1 \cdot a)\cdot(2 \cdot a)\cdot\dots\cdot ((p-1) \cdot a) \pmod,
既
W \equiv W\cdot a^ \pmod,
在這裡W=1•2•3•...•(p-1)。將整個公式除以W既得到:
a^ \equiv 1 \pmod
廣義
費馬小定理是歐拉定理的一個特殊情況:假如n和a的最大公約數是1的話,那么
a^{\varphi (n)} \equiv 1 \pmod
在這裡φ(n)是歐拉商數。歐拉商數的值是所有小於n的自然數中與n沒有公約數的數的量。假如n是一個質數,則φ(n) = n-1,即費馬小定理。
在費馬小定理的基礎上費馬提出了一種測試質數的算法。
實際套用
如上所述,中國猜測只有一半是正確的,符合中國猜測但不是質數的數被稱為偽質數。
假如所有符合1 < b < p的b p都滿足下列條件的話:
b^ \equiv b \mod p
則p必定是一個質數。
實際上沒有必要測試所有的小於p的自然數,只要測試所有的小於p的質數就可以了。
這個算法的缺點是它非常慢,運算率高。
相關理論
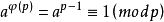 費馬小定理
費馬小定理費馬小定理是初等數論四大定理(威爾遜定理,歐拉定理(數論中的歐拉定理),中國剩餘定理(又稱孫子定理)和費馬小定理)之一,在初等數論中有著非常廣泛和重要的套用。實際上,它是歐拉定理的一個特殊情況(即
,見於詞條“歐拉函式”)。
卡麥可數
如上所述,中國猜測只有一半是正確的,符合中國猜測但不是質數的數被稱為“偽質數”。
更極端的反例是卡麥可數:
假設a與561互質,則a^560被561除都餘1。這樣的數被稱為卡麥可數數,561是最小的卡麥可數。Korselt在1899年就給出了卡麥可數的等價定義,但直到1910年才由卡麥可(Robert Daniel Carmichael)發現第一個卡麥可數:561。1994年William Alford 、 Andrew Granville 及 Carl Pomerance證明了卡麥可數有無窮多個。
費馬小定理的實際套用
如上所述,中國猜測只有一半是正確的,符合中國猜測但不是質數的數被稱為“偽質數”。
對於中國猜測稍作改動,即得到判斷一個數是否為質數的一個方法:
如果對於任意滿足1 < b < p的b下式都成立:
b^(p-1)≡1(mod p)
則p必定是一個質數。
實際上,沒有必要測試所有的小於p的自然數,只要測試所有的小於p的質數就可以了。
這個算法的缺點是它非常慢,運算率高;但是它很適合在計算機上面運行程式進行驗算一個數是否是質數。

