諾頓定律

諾頓定理：一個含獨立電源、線性電阻和受控源的二端電路N，對兩個端子來說都可等效為一個理想電流源並聯內阻的模型。其理想電流源的數值為有源二端電路N的兩個端子短路時其上的電流，並聯的內阻等於N內部所有獨立源為零時電路兩端子間的等效電阻。電路的這種特性，我們稱之為諾頓定理。

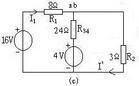
定義

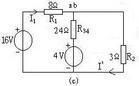諾頓定理示意圖

諾頓定律：任一一個有源線性單口網路，就其對外電路的作用而言，總可以用一個理想電流源和一個電阻並聯來等效，通常把電流源與電阻的並聯組合稱為諾頓等效電路。它是戴維南定律的轉換形式

諾頓定理得到一個理想電流源I與一個電導G並聯聯（習慣上與電流源對應使用的都用電導，不用電阻，當然這只是叫法不同而已）
戴維南定理得到一個理想電壓源U與一個電阻R串聯
兩者的轉換關係為GR=1（即諾頓定理得到的電阻與戴維南定理得到的電阻的阻值相等），且U=IR（即諾頓定理得到的電流源的電流、電阻與戴維南定理得到的電壓源電壓形式上滿足歐姆定律）

實例

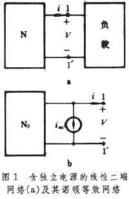
諾頓定理是與戴維南定理互為對偶的定理。定理指出，一個含有獨立電源線性二端網路N(圖1a),就其外部狀態而言,可以用一個獨立電流源isc和一個鬆弛二端網路N0的並聯組合來等效(圖1b)。其中，isc是網路N的短路電流，鬆弛網路N0是將網路N中的全部獨立電源和所有動態元件上的初始條件置零後得到的網路。上述並聯組合稱為諾頓等效網路。在復頻域中等效網路由電流源Isc和運算元阻抗Yi(s)並聯而成（圖2）。Isc(s)是短路電流的拉普拉斯變換，Yi(s)是鬆弛網路N0的入端（策動點）導納。另外，還能導出網路N用於正弦穩態分析和直流分板的等效網路。求等效電路的關鍵是求出網路N的短路電流和網路N0的入端（策動點）導納。它們均可通過電子計算機求得。

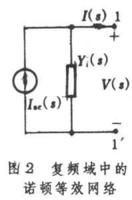諾頓定理

諾頓定理