簡介
 菱形
菱形圖像特性
對角線互相垂直平分。
 菱形背景
菱形背景正方形是特殊的菱形。
菱形面積為對角線相乘乘以二(鷂形面積):A=\frac\cdot x\cdot y;
或邊長的平方乘以其中一隻角的正弦(平行四邊形面積):A=a^2\cdot\sin\alpha。
菱形周界為邊長的四倍:U=4\cdot a
內接圓半徑:
r=\frac\cdot a\cdot\sin\alpha。
性質
1、對角線互相垂直且平分,並且每條對角線平分一組對角;
2、四條邊都相等;
3、對角相等,鄰角互補;
4、每條對角線平分一組對角,
5、菱形既是軸對稱圖形,對稱軸是兩條對角線所在直線,也是中心對稱圖形,
6、在60°的菱形中,短對角線等於邊長,長對角線是短對角線的√3倍。
7、菱形具備平行四邊形的一切性質。
判定
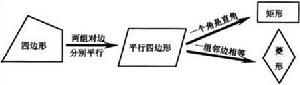
1、一組鄰邊相等的平行四邊形是菱形;
2、四邊相等的四邊形是菱形;
3、關於兩條對角線都成軸對稱的四邊形是菱形;
4、對角線互相垂直且平分的四邊形是菱形.。依次連線四邊形各邊中點所得的四邊形稱為中點四邊形。
不管原四邊形的形狀怎樣改變,中點四邊形的形狀始終是平行四邊形。
菱形的中點四邊形是矩形(對角線互相垂直的四邊形的中點四邊形定為矩形,對角線相等的四邊形的中點四邊形定為菱形。)。
菱形是在平行四邊形的前提下定義的,首先它是平行四邊形,但它是特殊的平行四邊形,特殊之處就是“有一組鄰邊相等”,因而就增加了一些特殊的性質和不同於平行四邊形的判定方法。
特點
順次連線菱形各邊中點為矩形
正方形是特殊的菱形,菱形不一定是正方形,所以,在同一平面上四邊相等的圖形不只是正方形。
圖形學約束
菱形必須一條對角線與x軸平行,另一條對角線與Y軸平行。
生活菱形
如手帕紙.拉門,衣帽架、紅色的貼圖(如“福”)等菱形面積
1.對角線乘積的一半(只要是對角線互相垂直的四邊形都可用);由把菱形分解成2個三角形,化簡得出2.底乘高=菱形面積。
3.設菱形的邊長為a,一個夾角為x°,則面積公式是:S=a²·sinx

