Sobolev嵌入定理
令W( R)表示包含 R上所有滿足前k階弱導數屬於L的實值函式的Sobolev空間。其中k是非負整數且有1 ≤p< ∞。Sobolev嵌入定理的第一部分指出如果k>ℓ且滿足1 ≤p<q< ∞和(k−ℓ)p<n
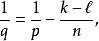索博列夫不等式那么
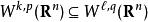索博列夫不等式並且該嵌入連續。在k= 1且ℓ= 0的特殊情形，Sobolev嵌入定理給出
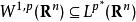索博列夫不等式其中p是p的Sobolev共軛，如下給出
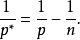索博列夫不等式這個Sobolev嵌入定理的特例可由Gagliardo–Nirenberg–Sobolev不等式直接得出。
Sobolev嵌入定理的第二部分用於嵌入到Hölder空間C( R)。如果(k−r−α)/n= 1/p其中α∈ (0, 1)，則有嵌入
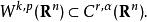索博列夫不等式Sobolev嵌入的這個部分可由Morrey不等式直接得出。直觀的說，這種包含關係表示足夠高階的弱導數存在性意味著一些經典導數的連續性。
一般Sobolev不等式
令U為 R上帶有 邊界的有界開集。（U也可以無界，但這種情況下，它的邊界如果存在，則必須是充分好的。）假設 ∈ ( )，考慮兩種情況：
k<n/p
這時u∈L(U)，其中
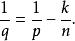索博列夫不等式有估計
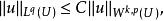索博列夫不等式常數C只依賴於k,p,n和U。
k>n/p
這裡u屬於Hölder空間，更精確的：
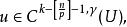索博列夫不等式其中
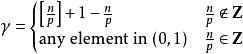索博列夫不等式有估計
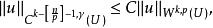索博列夫不等式常數C只依賴於k,p,n,γ和U。
p=n,k=1情形
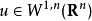索博列夫不等式如果 ，則u是有界平均振動函式且有
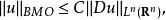索博列夫不等式對於某個常數C只依賴於n。這個估計是龐加萊不等式的推論。
Morrey不等式
假設n<p≤ ∞。存在常數C只依賴於p和n，使得
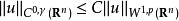索博列夫不等式 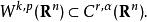索博列夫不等式對所有u∈C( R) ∩L( R)，其中
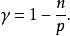索博列夫不等式因此如果u∈W( R)，則u在一個零測集上重新定義後，實際上為指數γ的Hölder連續。
一個類似的結果在帶有C邊界的有界定義域U上成立。此時，
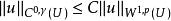索博列夫不等式其中常數C現在依賴於n,p和U。這一不等式可由前一不等式利用從W(U)到W( R)的保范延拓得到。
納什不等式
納什不等式，由約翰·納什引入，指出存在一個常數C> 0，滿足對所有u∈L( R) ∩W( R),
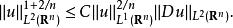索博列夫不等式這個不等式由傅立葉變換的基本性質導出。實際上，在半徑為ρ的球的補集上的積分，
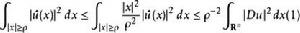索博列夫不等式由帕塞瓦爾定理。另一方面，有
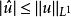索博列夫不等式在半徑為ρ的球上的積分給出
其中ω是n維球的體積。選擇ρ最小化( 1)和( 2)的和，再次使用帕塞瓦爾定理：
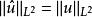索博列夫不等式給出不等式。
在n= 1的特殊情形，納什不等式可以擴展到L情形，此時是Gagliardo-Nirenberg-Sobolev不等式的推廣。實際上，如果I是有界區間，則對所有1 ≤r< ∞和所有1 ≤q≤p< ∞如下不等式成立
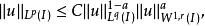索博列夫不等式其中
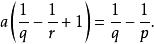索博列夫不等式