概念
梯度投影法(gradient projection method)利用梯度的投影技巧求約束非線性規劃問題最優解的一種方法。
求帶線性約束的非線性規劃問題更為有效。它是從一個基本可行解開始,由約束條件確定出凸約束集邊界上梯度的投影,以便求出下次的搜尋方向和步長。每次搜尋後,都要進行檢驗,直到滿足精度要求為止。這種方法是羅森於1960年提出的,戈德福布和拉匹塔斯於1968年作了改進。
基本原理
考慮最最佳化問題
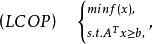 梯度投影法
梯度投影法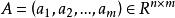 梯度投影法
梯度投影法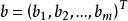 梯度投影法
梯度投影法其中 , 。
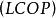 梯度投影法
梯度投影法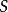 梯度投影法
梯度投影法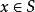 梯度投影法
梯度投影法的可行域記為 ,對任意 ,令
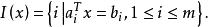 梯度投影法
梯度投影法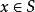 梯度投影法
梯度投影法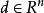 梯度投影法
梯度投影法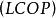 梯度投影法
梯度投影法 梯度投影法
梯度投影法定理1:設 ,則 為 在 處的可行方向的充分必要條件是
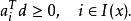 梯度投影法
梯度投影法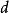 梯度投影法
梯度投影法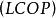 梯度投影法
梯度投影法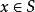 梯度投影法
梯度投影法推論1:設 是 在 處的可行方向,令
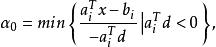 梯度投影法
梯度投影法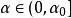 梯度投影法
梯度投影法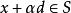 梯度投影法
梯度投影法則對任意 ,有 。
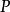 梯度投影法
梯度投影法 梯度投影法
梯度投影法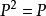 梯度投影法
梯度投影法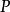 梯度投影法
梯度投影法定義1:設 是 階實對稱矩陣,如果 ,則稱 是投影矩陣。
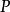 梯度投影法
梯度投影法 梯度投影法
梯度投影法定理2:設 是 階投影矩陣,則
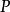 梯度投影法
梯度投影法(1) 是半正定矩陣;
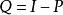 梯度投影法
梯度投影法(2) 也是投影矩陣;
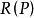 梯度投影法
梯度投影法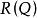 梯度投影法
梯度投影法(3)線性子空間 與 正交,其中
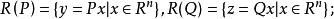 梯度投影法
梯度投影法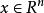 梯度投影法
梯度投影法(4)對任意 ,有唯一分解式
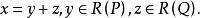 梯度投影法
梯度投影法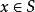 梯度投影法
梯度投影法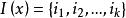 梯度投影法
梯度投影法定理3:設 且 ,記
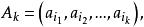 梯度投影法
梯度投影法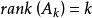 梯度投影法
梯度投影法如果 ,則
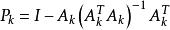 梯度投影法
梯度投影法(1) 是投影矩陣;
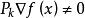 梯度投影法
梯度投影法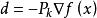 梯度投影法
梯度投影法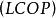 梯度投影法
梯度投影法 梯度投影法
梯度投影法(2)當 時, 是 在 處的可行下降方向。
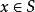 梯度投影法
梯度投影法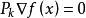 梯度投影法
梯度投影法定理4:設滿足定理3的條件且,令
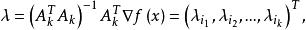 梯度投影法
梯度投影法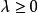 梯度投影法
梯度投影法 梯度投影法
梯度投影法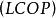 梯度投影法
梯度投影法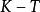 梯度投影法
梯度投影法(1)如果,則是的點;
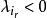 梯度投影法
梯度投影法(2)如果,令
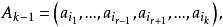 梯度投影法
梯度投影法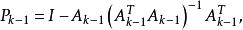 梯度投影法
梯度投影法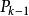 梯度投影法
梯度投影法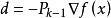 梯度投影法
梯度投影法 梯度投影法
梯度投影法 梯度投影法
梯度投影法則是投影矩陣,且是在處的可行下降方向。

