簡介
有限差分是形式為f(x+b)-f(x+a)的數學表達式。如果有限差分除以b-a,則得到差商。 有限差分導數的逼近在微分方程數值解的有限差分方法,特別是邊界值問題,起著關鍵的作用。
某些遞歸關係可以用有限差分代替疊代符號寫成差分方程。
而目前,“有限差分”這個詞通常被認為是有限差分的導數的近似同義詞,即有限差分商。尤其是在數值方法中 ,有限差分法是一種常用的數值解法,它是在微分方程中用差商代替偏導數,得到相應的差分方程,通過解差分方程得到微分方程解的近似值。地球物理正演模擬時常套用這種方法。
三種形式
有限差分通常考慮三種形式:正向,反向和中心差分 。
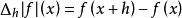 有限差分
有限差分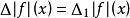 有限差分
有限差分正向差分的表達形式:,根據套用,間距h可以是可變的或恆定的。 省略時,h取為1:。
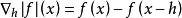 有限差分
有限差分反向差分使用在x,x−h之間的函式值,而不是在x+h,x之間的值:。
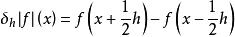 有限差分
有限差分中心差分則是,。
與導數的關係
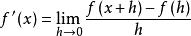 有限差分
有限差分函式f在點x的導數是由極限定義的,。
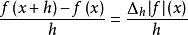 有限差分
有限差分如果h有一個固定的(非零)值,而不是趨近於零,那么上述方程的右邊就會寫出來,。
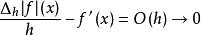 有限差分
有限差分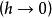 有限差分
有限差分因此,正向差分除以h近似於h很小的導數。這個近似的誤差可以從泰勒定理得到。假設f是可微的,我們有當。
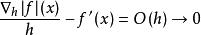 有限差分
有限差分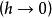 有限差分
有限差分同樣的公式適用於反向差分:當。
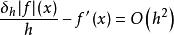 有限差分
有限差分然而,中心差分產生了一個更精確的近似。如果f是可微的,。
然而,中心差分法的主要問題是振盪函式可以產生零導數。如果用中心差分計算的話,n奇數時,f(nh)= 1 ;n為偶數時,f(nh)= 2,那么f '(nh)= 0。如果f的域是離散的,這就更複雜。
有專家認為,有限差分近似定義了正/反向/中心差分 。
有限差分的推廣
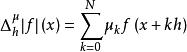 有限差分
有限差分廣義有限差分通常定義為。
其中μ=(μ,…,μ)是它的係數向量。在這裡有限差分被一個無窮級數取代。另一種泛化方法是使係數μ依賴於點x:μ=μ(x),因此考慮加權有限差分。同樣,也可以使h依賴於點x:h = h(x)。這樣的概括對於構造不同的連續性模量是很有用的。
套用
有限差分法又稱差分方法。一種以差商代替微商,以差分 方程逼近微分方程,通過求格線點上的函式值來求 解偏微分 (或常微分) 方程和方程組定解問題的數值解法。基本作法是: 把問題的定義域進行格線剖 分,然後在格線點上,按適當的數值微分公式把定 解問題中的微商換成差商,從而把原問題離散化為 差分格式 (亦稱差分方程),進而求出數值解。方 法具有簡單、靈活以及通用性強等特點,容易在計 算機上實現; 是解各類數學物理問題的主要數值方 法,也是計算力學中的主要數值方法之一。在固體 力學中,有限元法出現以前,主要採用差分方法; 在流體力學中,仍然是主要的數值方法,對依賴於 時間發展的方程,更是如此。
在桿繫結構穩定中,將穩定問題中的中性平衡 微分方程近似地用差分方程代替以確定臨界荷載的 一種數值方法。宜與電子計算機配合套用。其要點 為: 先寫出該穩定問題的中性平衡微分方程,利用 差分公式把微分方程中未知函式υ(x) 的各階導 數 (或偏導數) 用有限個差分結點的函式值來表 示,從而將微分方程近似地用相應的差分方程組來 代替。這樣便把中性平衡微分方程化為含有n個 未知量的齊次線性代數方程組,據此可導出其穩定 方程,進而可求得臨界荷載的近似解。所取差分結 點越多,計算結果越精確。它屬於套用靜力準則求 解穩定問題的近似法。為了提高計算精度,常輔以 里查森外推法。用有限差分法只能求得臨界荷載的 近似值而不能得到撓度函式υ(x)的表達式。
求解微分方程
簡稱差分法或格線法,是求微分方程和積分一微分方程的數值解的一種主要的計算方法。它的基本思想是:把連續的定解區域用由有限個離散點構成的格線來代替,這些離散點被稱為格線的結(節)點;把在連續定解區域上定義的連續變數函式用在格線上定義的離散變數函式來近似;把原方程和定解條件中的微商用差商來近似,積分用積分和來近似。於是原方程和定解條件就可用代數方程組來近似地代替,解此代數方程組就得到原問題的近似解。這種方法簡單、通用,易於在電子計算機上實現。
有限差分方法有漫長的歷史,源於牛頓、歐拉等人的工作,他們曾用差商代替微商以簡化計算。1928年,庫朗、盧伊等人證明了三大典型方程的典型差分格式的收斂性定理,為現代有限差分理論提供了基礎。同時,庫朗把有限差分法用於求偏微分方程的數值解,發展了這一方法。由於有限差分方法具有通用性,又便於機器實現,因而在電子計算機產生和廣泛套用後更得到很大發展及更廣泛的套用。馮 ·諾伊曼於1948年對無粘流體(非線性雙曲型)方程提出的引入人工粘性項的差分方法是一個典型例子,他還同時提出計算穩定性概念和線性化傅立葉方法來分析穩定性。後來拉克斯等人建立了一般差分格式的收斂性、穩定性等價定理。人工粘性法成為現代流體計算的主導方法之一,而得出這種方法的自適應的算法思想也給其他計算方法的發展以很大的啟發和影響。在現代,有限差分方法套用於各類微分方程和積分—微分方程的各種定解問題,如常微分方程初值問題、邊值問題,偏微分方程初值問題、邊值問題,玻耳茲曼方程,計算流體力學等等。它是把微分方程離散化,從而求其數值解的基本方法之一。
