定義
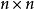拉普拉斯展開 
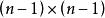拉普拉斯展開 在數學中，拉普拉斯展開（或稱拉普拉斯公式）是一個關於行列式的展開式。將一個 矩陣 B的行列式進行拉普拉斯展開，即是將其表示成關於矩陣 B的某一行（或某一列）的 n個元素的 餘子式的和。行列式的拉普拉斯展開一般被簡稱為行列式按某一行（或按某一列）的展開。由於矩陣 B有 n行 n列，它的拉普拉斯展開一共有 2 n種。拉普拉斯展開的推廣稱為拉普拉斯定理，是將一行的元素推廣為關於 k行的一切子式。它們的每一項和對應的代數餘子式的乘積之和仍然是 B的行列式。研究一些特定的展開可以減少對於矩陣 B之行列式的計算，拉普拉斯公式也常用於一些抽象的推導中。
公式
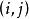拉普拉斯展開 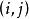拉普拉斯展開 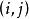拉普拉斯展開 設 B= ( b)是一個 n× n矩陣。 B關於第 i行第 j列的餘子式 M是指 B中去掉第 i行第 j列後得到的 n−1階子矩陣的行列式。有時可以簡稱為 B的 餘子式。 B的 代數餘子式： C是指 B的 餘子式 M與(−1)的乘積：
C= (−1) M
拉普拉斯展開最初由范德蒙德給出，為如下公式：對於任意 i, j∈ {1, 2, ..., n}：
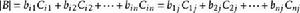拉普拉斯展開 考慮以下的矩陣：
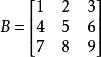拉普拉斯展開 這個矩陣的行列式可以用沿著第一行的拉普拉斯展開式來計算：
拉普拉斯展開 也可以用沿著第二列的拉普拉斯展開式來計算：
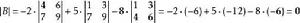拉普拉斯展開 很容易看到這個結果是正確的：這個矩陣是奇異的，因為它的第一列和第三列的和與第二列成比例，因此它的行列式是零。
證明
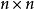拉普拉斯展開 
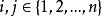拉普拉斯展開 
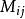拉普拉斯展開 
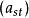拉普拉斯展開 
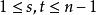拉普拉斯展開 設 B是一個 的矩陣， 。為了明確起見，將 的係數記為 ，其中 。
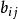拉普拉斯展開 考慮 B的行列式 |B|中的每個含有 的項，它的形式為：
拉普拉斯展開 其中的置換τ ∈ S使得τ( i) = j，而σ ∈ S是唯一的將除了 i以外的其他元素都映射到與τ相同的像上去的置換。顯然，每個τ都對應著唯一的σ，每一個σ也對應著唯一的τ。因此我們創建了 S與{τ∈ S:τ( i)= j}之間的一個雙射。置換τ可以經過如下方式從σ得到：
定義σ' ∈ S使得對於1 ≤ k≤ n−1，σ'( k) = σ( k)並且σ'( n) = n，於是sgnσ' = sgn σ。然後
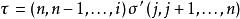拉普拉斯展開 
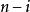拉普拉斯展開 
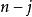拉普拉斯展開 由於兩個輪換分別可以被寫成 和 個對換，因此
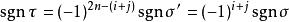拉普拉斯展開 因此映射σ ↔ τ是雙射。由此：
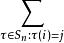拉普拉斯展開 
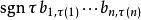拉普拉斯展開 
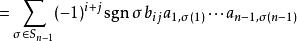拉普拉斯展開 
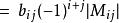拉普拉斯展開 從而拉普拉斯展開成立。
相關定理
拉普拉斯定理
拉普拉斯在1772年的論文中給出了行列式展開的一般形式，現在稱為拉普拉斯定理。拉普拉斯定理建立在子式和餘子式的基礎上，說明了如果將 B關於某k行的每一個子式和對應的代數餘子式的乘積加起來，那么得到的仍然是 B的行列式。定理的證明與按一行（一列）展開的情況一樣，都是通過建立置換間的雙射來證明兩者相等。
