抽象指標記號

抽象指標記號（英語：abstract index notation）是由羅傑·彭羅斯發明的一種用來表示張量與旋量的數學記號。

簡介

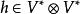抽象指標記號

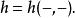抽象指標記號

假定 V為向量空間， V是其對偶空間。定義二階協變張量 ，則 h是 V上的雙線性映射，即可表示為（以兩個“槽”表示 V中的兩個變數）：

抽象指標記號便是通過拉丁字母代替“槽”來表示上式：

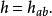抽象指標記號

當協變指標（下標，表示 V中張量）與逆變指標（上標，表示 V中張量）重複時表示進行縮並運算，如：

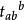抽象指標記號

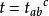抽象指標記號

即表示 對後兩個“槽”進行縮並的跡。這種表示縮並的方式與愛因斯坦求和約定類似，但此表示法只是抽象的記號而已，並不表示求和運算。

特徵

與不帶指標的字母（如 T）表示張量相比，抽象指標記號表示法能夠顯示張量的類型，同時可清楚地表明縮並等運算。而與用分量（張量在某一特定基底下的分量）表示張量不同，該表示法與特定的基底無關，可以表示出張量等式。