簡介
扭曲幾何寫成如下形式的黎曼流形或洛倫茲流形：
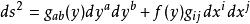扭曲幾何注意到幾何可以分解成y幾何與x幾何的卡氏積（Cartesian product），不過x部分受到扭曲，亦即它的大小尺度受到了一個y坐標的標量函式{\displaystyle f(y)}的調整。基於此理由，扭曲幾何的度規常稱為“扭曲積度規”（warped product metric）。
扭曲幾何很有用處，以其可以運用分離變數法來解與它們有關的偏微分方程。
例子
許多愛因斯坦場方程的基本解是為扭曲幾何，比如史瓦西解以及羅伯遜-沃爾克模型。
此外，扭曲幾何是弦論中藍道爾-桑壯模型（Randall-Sundrum models）的基石。
相關內容
度量張量
在黎曼幾何裡面，度量張量（英語：Metric tensor）又叫黎曼度量，物理學譯為度規張量，是指一用來衡量度量空間中距離，面積及角度的二階張量。
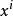扭曲幾何
扭曲幾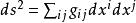何
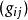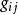扭曲幾何
扭曲幾何當選定一個局部坐標系統 ，度量張量為二階張量一般表示為 ，也可以用矩陣 表示，記作為G或g。而 記號傳統地表示度量張量的協變分量（亦為“矩陣元素”）。
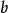扭曲幾何
扭曲幾何到 的弧線長度定義如下，其中參數定為t，t由a到b:
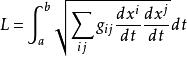扭曲幾何
扭曲幾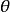何
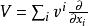扭曲幾何
扭曲幾何兩個切矢量的夾角 ,設矢量 和 ，定義為：
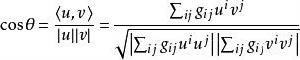扭曲幾何
扭曲幾何
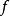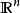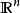扭曲幾何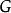 扭曲幾何
扭曲幾何若 為 到 的局部微分同胚，其誘導出的度量張量的矩陣形式 ，由以下方程計算得出：
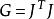扭曲幾何 扭曲幾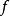何
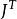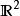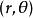扭曲幾何
扭曲幾何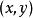
扭曲幾何
扭曲幾何j表示 的雅可比矩陣，它的轉置為 。著名例子有 之間從極坐標 到直角坐標 的坐標變換，在這例子裡有：
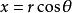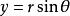扭曲幾何
扭曲幾何這映射的雅可比矩陣為
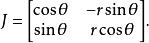扭曲幾何所以
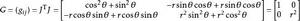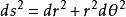扭曲幾何
扭曲幾何這跟微積分里極坐標的黎曼度量, ，一致。
