托爾曼-奧本海默-沃爾科夫極限

托爾曼-奧本海默-沃爾科夫極限

確定後，托爾曼-奧本海默-沃爾科夫方程能夠完全決定這個球對稱且各向同性的系統在引力平衡狀態下的結構。 托爾曼-奧本海默-沃爾科夫方程也因此特別叫做恆星的流體靜力學平衡方程。 一個由恆星坍縮成的黑洞必須具有大於托爾曼-奧本海默-沃爾科夫極限的質量。

羅伯特·奧本海默
天體物理學中，托爾曼-奧本海默-沃爾科夫方程（英文：Tolman-Oppenheimer-Volkoff Equation，簡稱作TOV Equation）是在廣義相對論框架下描述一個處在定態引力平衡狀態下的各向同性球對稱物體結構的約束方程。它所描述的是恆星在輻射壓力和自身引力作用下的相對論性流體靜力學平衡。

方程形式

方程的形式為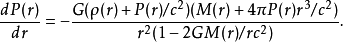
\frac{dP(r)}{dr}=-\frac{G(\rho(r)+P(r)/c^2)(M(r)+4\pi P(r)r^3/c^2)}{r^2(1-2GM(r)/rc^2)}.
這裡r\,是徑向坐標，而我們用\rho(r_0)\,和P(r_0)\,分別是物質在其半徑r = r_0\,處的密度和壓力。M(r_0)\,是在半徑r = r_0\,以內物質的總質量，這是從遠處的觀察者所觀察到的它的[[引力場]]的角度而言的（所謂遠處，是指那裡的度規不受到系統本身的引力場影響）。這個質量滿足M(0)=0\,，並且有
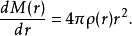
\frac{dM(r)}{dr}=4 \pi \rho(r) r^2.
這個方程的導出來自愛因斯坦引力場方程在一個廣義的定態且球對稱度規（不一定是史瓦西度規）條件下的解，具體討論的導出過程可參考這裡。這裡簡單敘述為，對於一個滿足托爾曼-奧本海默-沃爾科夫方程的解，度規具有如下形式
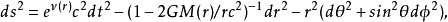
ds^2=e^{\nu(r)} c^2 dt^2 - (1-2GM(r)/rc^2)^{-1} dr^2 - r^2(d\theta^2 + sin^2 \theta d\phi^2),
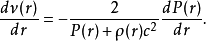
其中\nu(r)\,滿足約束條件\frac{d\nu(r)}{dr}=-\frac{2}{P(r)+\rho(r)c^2} \frac{dP(r)}{dr}.
當系統的狀態方程（EOS，它建立了密度與壓力的關係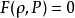）F(\rho, P) = 0\,確定後，托爾曼-奧本海默-沃爾科夫方程能夠完全決定這個球對稱且各向同性的系統在引力平衡狀態下的結構。注意到如果1/c^2\,項可忽略，托爾曼-奧本海默-沃爾科夫方程會退化成牛頓力學的流體靜力學方程，這是當相對論修正不重要時求解球對稱且各向同性的系統在引力平衡狀態下的結構所需要的方程。托爾曼-奧本海默-沃爾科夫方程也因此特別叫做恆星的流體靜力學平衡方程。
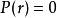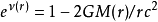如果這個方程被用來描述一個真空中的束縛星體，在邊界上需要套用零壓力條件P(r)=0\,以及條件e^{\nu(r)} = 1 - 2GM(r)/rc^2\,。第二個邊界條件是因為度規在邊界上需要連續，並且對真空中的愛因斯坦方程具有唯一的定態球對稱解——史瓦西度規：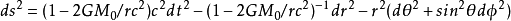
ds^2=(1-2GM_0/rc^2) c^2 dt^2 - (1-2GM_0/rc^2)^{-1} dr^2 - r^2(d\theta^2 + sin^2 \theta d\phi^2)\,
這裡M_0\,是星體的總質量，這仍然是從遠處的觀察者所觀察到的它的引力場的角度而言的。如果星體的邊界處於r\,，度規的連續性以及M(r)\,的定義都要求
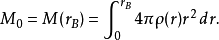
M_0=M(r_B)=\int_0^{r_B} 4\pi \rho(r) r^2\, dr.
但從另一方面看，如果考慮系統的引力場作用下的度規，將星體的密度在對應的體元下積分，將得到一個更大的質量函式
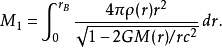
M_1=\int_0^{r_B} \frac{4\pi \rho(r) r^2}{\sqrt{1-2GM(r)/rc^2}} \, dr.
這兩個質量的差別為
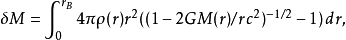
\delta m=\int_0^{r_B} 4\pi \rho(r) r^2((1-2GM(r)/rc^2)^{-1/2}-1)\, dr,
這個值是大於零的，體現了星體因引力作用產生的束縛能量，也就是將星體內部的物質打散後拋到無限遠處所要消耗的能量。

歷史

托爾曼（Richard C. Tolman）在1934年和1939年間分析了球對稱度規而這個方程的形式則是由奧本海默和沃爾科夫（George Volkoff）藉助托爾曼的工作在他們1939年的論文《在巨大的中子核上》中推導出的。在這篇論文中，他們採用了一個中子組成的簡併費米氣體模型的狀態方程來計算中子星質量的上限，其結果約為0.7倍太陽質量。由於他們所用的狀態方程對中子星而言並不理想，這個得到的極限應該是錯誤的，現代對這一極限的估計為1.5至3倍太陽質量。

托爾曼-奧本海默-沃爾科夫極限

白矮星-內部結構模型圖白矮星-內部結構模型圖
托爾曼-奧本海默-沃爾科夫極限（TOV極限，也叫奧本海默-沃爾科夫極限）即是中子星的質量上限，類似於白矮星質量上限的錢德拉塞卡極限。如上節所述，奧本海默和沃爾科夫得到的中子星質量上限約為0.7倍太陽質量，這在今天看來應該是錯誤的，當今的結果在1.5至3倍太陽質量之間。對於質量小於此極限的中子星，支持星體的內部壓力來自中子與中子之間的強相互作用以及中子本身的量子簡併壓力；而對於質量大於此極限的中子星會在自身引力的作用下崩潰，從而坍縮為一個黑洞，理論上在其他途徑的內部壓力支持下還可能成為其他形式的星體（例如在夸克簡併壓力的支持下坍縮為夸克星）。但由於對這些理論上的夸克簡併物質了解相對中子簡併物質更少，一般天體物理學家相信，除非有實際觀測的反例證實，中子星在超過這一極限時都會直接坍縮為黑洞。
中子星-內部結構模型圖中子星-內部結構模型圖

一個由恆星坍縮成的黑洞必須具有大於托爾曼-奧本海默-沃爾科夫極限的質量。理論預言由於恆星演化中的質量損失，一個具有太陽那樣金屬量的孤立恆星坍縮而成的黑洞應該具有不超過10倍左右的太陽質量。在錢德拉X射線天文台的實驗觀測中，有相當數量的X射線雙星由於它們的巨大質量、較低的亮度以及X射線光譜被認為是恆星質量黑洞，它們的質量據估計在3倍至20倍太陽質量之間 。
夸克星-內部結構模型圖夸克星-內部結構模型圖

相關詞條

熱門詞條

聯絡我們