射影定理

所謂射影，就是正投影。直角三角形射影定理（又叫歐幾里德(Euclid)定理）：直角三角形中，斜邊上的高是兩直角邊在斜邊上射影的比例中項。每一條直角邊是這條直角邊在斜邊上的射影和斜邊的比例中項。概述圖中，在Rt△ABC中，∠ABC=90°，BD是斜邊AC上的高，則有射影定理如下：BD²=AD·DC，AB²=AC·AD，BC²=CD·AC，由古希臘著名數學家、《幾何原本》作者歐幾里得提出。歐幾里得（希臘文：Ευκλειδης，公元前325年—公元前265年），古希臘數學家，被稱為“幾何之父”。他活躍於托勒密一世（公元前323年－公元前283年）時期的亞歷山大里亞。他最著名的著作《幾何原本》是歐洲數學的基礎，總結了平面幾何五大公設，被廣泛的認為是歷史上最成功的教科書。歐幾里得也寫了一些關於透視、圓錐曲線、球面幾何學及數論的作品。

基本信息

• 中文名稱：射影定理
• 外文名：Right triangle altitude theorem
• 別稱：歐幾里德定理 第一餘弦定理
• 表達式：BD²=AD·DC AB²=AC·AD BC²=CD·AC
• 提出者：歐幾里得
• 提出時間：公元前325年
• 套用學科：數學幾何
• 適用領域範圍：建築，測量，光學，航海，航空和製造業

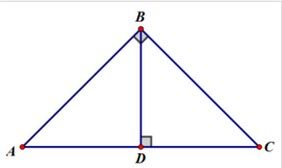
驗證推導

①CD^2=AD·BD;②AC^2=A
D·AB;③BC^2=BD·AB;④AC·BC=AB·CD

證明

∴2CD^2+AD^2+BD^2=AC^2+BC^2
∴2CD^2=AB^2-AD^2-BD^2
∴2CD^2=(AD+BD)^2-AD^2-BD^2
∴2CD^2=AD^2+2AD×BD+BD^2-AD^2-BD^2
∴2CD^2=2AD·BD
∴CD^2=AD·BD
②∵CD^2=AD·BD(已證)
∴CD^2+AD^2=AD·BD+AD^2
∴AC^2=AD·(BD+AD)
∴AC^2=AD·AB
③BC^2=CD^2+BD^2
BC^2=AD×BD+BD^2
BC^2=(AD+BD)·BD
BC^2=AB·BD
∴BC^2=AB·BD
④∵S△ACB=1/2AC×BC=1/2AB×CD
∴1/2AC×BC=1/2AB×CD
∴AC×BC=AB×CD

定理內容

射影定理的推廣證明

歐幾里得提出的面積射影定理規定“平面圖形射影面積等於被射影圖形的面積乘以該圖形所在平面與射影面所夾角的餘弦。(即COSθ=S射影/S原）。”
(平面多邊形及其射影的面積分別是和,它們所在平面所成的二面角為)

證明思路

正射影二面角的歐幾里得射影面積公式
因為射影就是將原圖形的長度（三角形中稱高）縮放，所以寬度是不變的，又因為平面多邊形的面積比=邊長的乘積比。所以就是圖形的長度（三角形中稱高）的比。
那么這個比值應該是平面所成角的餘弦值。在兩平面中作一直角三角形，並使斜邊和一直角邊垂直於棱（即原多邊形圖的平面和射影平面的交線），則三角形的斜邊和另一直角邊就是其多邊形的長度比，即為平面多邊形的面積比。將此比值放到該平面中的三角形中去運算即可得證。

發展簡史

直角三角形中的射影定理

歐幾里得（希臘文：Ευκλειδης，公元前325年—公元前265年），古希臘數學家，被稱為“幾何之父”。他活躍於托勒密一世（公元前323年－公元前283年）時期的亞歷山大里亞。他最著名的著作《幾何原本》是歐洲數學的基礎，總結了平面幾何五大公設，被廣泛的認為是歷史上最成功的教科書。歐幾里得也寫了一些關於透視、圓錐曲線、球面幾何學及數論的作品。

搞笑講解

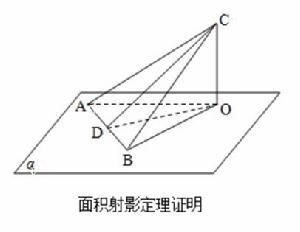面積射影定理

安倍在C點說：“釣魚島是日本的！”然後，他從C點通過陷阱CD摔到D點，然後摔得一分為二，一塊崩到A點，另一塊崩到B點。所以CD^2=AD·BD。
安倍又重蹈覆轍，於是他又從C點通過陷阱BC摔到B點，然後摔得一分為二，一塊崩到D點，另一塊崩到A點。BC^2=AB·BD。同理，他他又從C點通過陷阱AC摔到A點，然後摔得一分為二，一塊崩到D點，另一塊崩到B點。AC^2=AB·AD。
總之，陷阱距離的平方等於兩塊安倍屍體走的距離的乘積。