基本介紹
考慮標準型LP問題
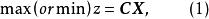 基本最優解
基本最優解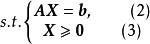 基本最優解
基本最優解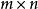 基本最優解
基本最優解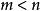 基本最優解
基本最優解設 A是階矩陣,,且 A的秩為m。
可行解:滿足上述約束條件(2)、(3)的向量x稱為可行解(feasible solution)。
最優解:滿足式(1)的可行解稱為最優解(optimal solution)。
基: A中任何一組m個線性無關的列向量構成的子矩陣 B,稱為該問題的一個基(basis),即 B為 A的m×m階非奇異子矩陣。
基向量:基 B中的一列即為 B的一個基向量。基 B中共有m個基向量。
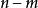 基本最優解
基本最優解非基向量:矩陣 A中基 B之外的一列即為 B的一個非基向量。 A中共有個非基向量。
基變數:與基 B的基向量相應的變數稱為 B的基變數。基變數共有m個。
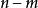 基本最優解
基本最優解非基變數:與基 B的非基向量相應的變數稱為 B的非基變數,非基變數共有個。
基本解:對於基 B,令所有非基變數為零,求得滿足式(2)的解,稱為 B對應的 基本解(basic solution)。
基本可行解:滿足式(3)的基本解稱為基本可行解,其對應的基稱為可行基。
基本最優解:滿足式(1)的基本可行解稱為基本最優解,其對應的基稱為最優基。
退化的基本解:若基本解中有基變數為零者,則稱之為退化的基本解。類似地,有退化的基本可行解和退化的基本最優解 。
求解方法
單純形方法是求解線性規劃問題的一個主要方法,構成了線性規劃理論的一個重要內容,其計算主要是由單純形表來實現的。
設線性規劃目標函式為:
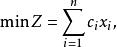 基本最優解
基本最優解約束條件為:
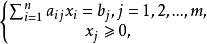 基本最優解
基本最優解其矩陣形式為:
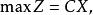 基本最優解
基本最優解 基本最優解
基本最優解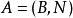 基本最優解
基本最優解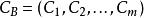 基本最優解
基本最優解令,其中B是秩為m的m階方陣,
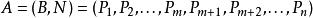 基本最優解
基本最優解那么稱,
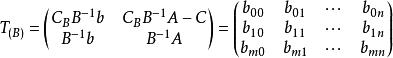 基本最優解
基本最優解基B對應的單純形表。
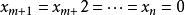 基本最優解
基本最優解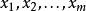 基本最優解
基本最優解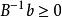 基本最優解
基本最優解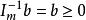 基本最優解
基本最優解表中第1列第1分量是對應於B基礎解即的目標函式值,其他m個分量就是對應於B的基礎解中基變數的值。表中第1行除第1分量外,其餘n個分量為檢驗數CBB A—C。對於可行基B(即)的表,如果所有檢驗數非正,那么這一基礎可行解就是最優解。第1個可行基一般取單位矩陣,這隻要在約束方程兩邊同乘以+1或-1,並引入和方程個數相同的人工變數,那么這m個人工變數對應的係數矩陣就是單位矩陣I,且滿足。
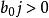 基本最優解
基本最優解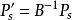 基本最優解
基本最優解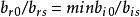 基本最優解
基本最優解如果有一個檢驗數大於零,那么就需要換基疊代,其步驟是:(1)求主元素。在所有中,選最靠左的一個,記為b,其對應的非基變數x,對應於向量,用P'列正的各分量b分別去除b,,稱b為主元素。(2)對B的單純形表進行變換使P'變為單位向量(第r個分量為1,其餘為0),將P'與第r列對調,即將一個新基的單純形表。那么換基後目標函式值不會增加,只有在下述情形原問題無最優解:檢驗數b中有正數,且無對應的列向量是負向量 。

