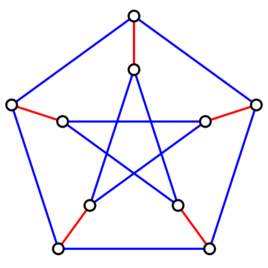
概述
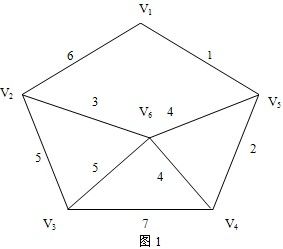 圖論
圖論圖論本身是套用數學的一部份,因此,歷史上圖論曾經被好多位數學家各自獨立地建立過。關於圖論的文字記載最早出現在歐拉1736年的論著中,他所考慮的原始問題有很強的實際背景。
起源
眾所周知,圖論起源於一個非常經典的問題——柯尼斯堡(Konigsberg)問題。1738年,瑞典數學家歐拉(LeornhardEuler)解決了柯尼斯堡問題。由此圖論誕生。歐拉也成為圖論的創始人。
1859年,英國數學家漢密爾頓發明了一種遊戲:用一個規則的實心十二面體,它的20個頂點標出世界著名的20個城市,要求遊戲者找一條沿著各邊通過每個頂點剛好一次的閉迴路,即“繞行世界”。用圖論的語言來說,遊戲的目的是在十二面體的圖中找出一個生成圈。這個生成圈後來被稱為漢密爾頓迴路。這個問題後來就叫做漢密爾頓問題。由於運籌學、計算機科學和編碼理論中的很多問題都可以化為漢密爾頓問題,從而引起廣泛的注意和研究。
猜想
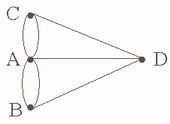 圖論
圖論雖然四色定理證明了任何地圖可以只用四個顏色著色,但是這個結論對於現實上的套用卻相當有限。現實中的地圖常會出現飛地,即兩個不連通的區域屬於同一個國家的情況(例如美國的阿拉斯加州),而製作地圖時我們仍會要求這兩個區域被塗上同樣的顏色,在這種情況下,四個顏色將會是不夠用的。
20世紀80-90年代曾邦哲的綜合系統論(結構論)觀將“四色猜想”命題轉換等價為“互鄰面最大的多面體是四面體”。每個地圖可以導出一個圖,其中國家都是點,當相應的兩個國家相鄰時這兩個點用一條線來連線。所以四色猜想是圖論中的一個問題。它對圖的著色理論、平面圖理論、代數拓撲圖論等分支的發展起到推動作用。
(下圖是在上下對摺再左右對摺以後形成一個輪胎形狀,有7個區域兩兩相連,就是說在一個環面上作圖,需要7種顏色,外國數學家構造林格證明:Np=[(7+√1+48p)/2],p=1,N1=7。
圖論的廣泛套用,促進了它自身的發展。20世紀40-60年代,擬陣理論、超圖理論、極圖理論,以及代數圖論、拓撲圖論等都有很大的發展。
拓撲學
幾何拓撲學是十九世紀形成的一門數學分支,它屬於幾何學的範疇。有關拓撲學的一些內容早在十八世紀就出現了。那時候發現一些孤立的問題,後來在拓撲學的形成中占著重要的地位。在數學上,關於哥尼斯堡七橋問題、多面體的歐拉定理、四色問題等都是拓撲學發展史的重要問題。
哥尼斯堡(今俄羅斯加里寧格勒)是東普魯士的首都,普萊格爾河橫貫其中。十八世紀在這條河上建有七座橋,將河中間的兩個島和河岸聯結起來。人們閒暇時經常在這上邊散步,一天有人提出:能不能每座橋都只走一遍,最後又回到原來的位置。這個問題看起來很簡單有很有趣的問題吸引了大家,很多人在嘗試各種各樣的走法,但誰也沒有做到。看來要得到一個明確、理想的答案還不那么容易。
1736年,有人帶著這個問題找到了當時的大數學家歐拉,歐拉經過一番思考,很快就用一種獨特的方法給出了解答。歐拉把這個問題首先簡化,他把兩座小島和河的兩岸分別看作四個點,而把七座橋看作這四個點之間的連線。那么這個問題就簡化成,能不能用一筆就把這個圖形畫出來。經過進一步的分析,歐拉得出結論--不可能每座橋都走一遍,最後回到原來的位置。並且給出了所有能夠一筆畫出來的圖形所應具有的條件。這是拓撲學的“先聲”。
在拓撲學的發展歷史中,還有一個著名而且重要的關於多面體的定理也和歐拉有關。這個定理內容是:如果一個凸多面體的頂點數是v、棱數是e、面數是f,那么它們總有這樣的關係:f+v-e=2。
根據多面體的歐拉定理,可以得出這樣一個有趣的事實:只存在五種正多面體。它們是正四面體、正六面體、正八面體、正十二面體、正二十面體。