啞指標

矢量和張量分析中，啞指標和愛因斯坦求和約定聯繫在一起。矢量分析中，在一個單項式內，同時出現且僅出現兩次的指標為啞指標。對這種指標應當進行遍歷求和。啞指標定義了一種運算法則，即按照愛因斯坦求和約定，當啞指標出現時，必須把該項在該指標的取值範圍內遍歷求和。相對地，在某一多項式中出現次數不為2的下標，稱為自由指標。在張量分析中的定義是：一個單項式內，在上標（向量指標）和下標（余向量指標）中各出現且僅出現1次的指標稱為啞指標。

定義

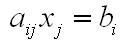啞指標

矢量分析中，在表達式的某一單項式之中出現且僅出現2次的下標，稱為啞指標。

相對地，在某一多項式中出現次數不為2的下標，稱為自由指標。

例如，在右圖中的表達式，j 為啞指標，在三維問題中，其變化範圍為1，2，3。

而 i 雖然出現了2次，但並不處於同一個多項式內，是自由指標。

在張量分析中的定義是：一個單項式內，在上標（向量指標）和下標（余向量指標）中各出現且僅出現1次的指標稱為啞指標。

愛因斯坦求和約定

啞指標

啞指標定義了一種運算法則，即按照愛因斯坦求和約定，當啞指標出現時，必須把該項在該指標的取值範圍內遍歷求和。

啞指標

例如，在三維空間中，對於向量

和

而言，

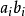啞指標

實際上代表

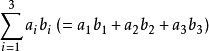啞指標

而自由指標則代表，在該指標所可遍歷的範圍內，等式均成立。例如，三維直角坐標系中，

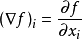啞指標

實際上代表

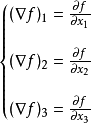啞指標

或

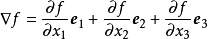啞指標