定理敘述
 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理設為一個測度空間,是一個實值的可測函式列。 如果逐點收斂於一個函式,並存在一個勒貝格可積的函式,使得對每個,任意,都有:
 勒貝格有界收斂定理
勒貝格有界收斂定理則:
 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理也是勒貝格可積的,;
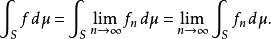 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理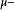 勒貝格有界收斂定理
勒貝格有界收斂定理其中的函式一般取為正值函式。函式列的逐點收斂和的性質可以減弱為幾乎處處成立。
證明
勒貝格控制收斂定理是更廣泛的法圖-勒貝格定理(Fatou–Lebesgue theorem)的特例。以下是一個套用法圖引理的證明。
 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理由於 是逐點收斂的極限,因此對其仍然有
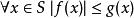 勒貝格有界收斂定理
勒貝格有界收斂定理 勒貝格有界收斂定理
勒貝格有界收斂定理(於是)。
同理,對任意的 n有:
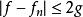 勒貝格有界收斂定理
勒貝格有界收斂定理以及
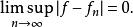 勒貝格有界收斂定理
勒貝格有界收斂定理根據法圖引理,可以得到:
 勒貝格有界收斂定理
勒貝格有界收斂定理因此,由勒貝格積分的線性性和單調性,就有:
 勒貝格有界收斂定理
勒貝格有界收斂定理而後者趨於0,於是定理得證。

