定義
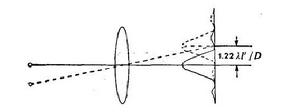 雙點的分辨
雙點的分辨如圖的光學系統,物是由兩個輻射強度相等的不相干點光源所組成。這個光學系統是衍射受限的,意恩是,兩點的象幾乎恰好都是孔徑的夫琅和費衍射圖樣。
當兩點問的距離很遠時,兩個衍射圖樣也同樣相距很遠,我們能夠清楚地分辨兩點。當兩點互相移近時,有限擴展的衍射圖樣就會重迭起來。當重迭足夠大時,兩點就不能分辨了。
我們現在研究兩個象的分辨極限問題。這就是分清兩點的兩個衍射圖樣閥的最小距離。通常套用瑞利判據,它規定當一點的衍射極大與另一點的第一衍射極小相重合時,剛好能分辨兩點。
即使透鏡沒有象差,一個物點的成象也並不是被透鏡折射的諸光線的簡單相交,而是呈現一種衍射圖樣,因此,透鏡的分辨有一個最終極限。如果一透鏡或一光學系統能把兩物點的相應衍射圖樣分得足夠開,我們就說它們能分辨這兩個物點。
分辨極限的判定
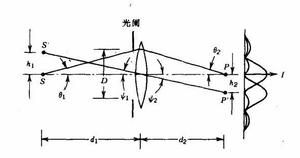 透鏡的分辨極限
透鏡的分辨極限光學成象系統或單透鏡對兩個靠得很近的物的成象,如圖所示。假設透鏡是消象散的,即從物點S出射到透鏡 上的任何一條光線都將通過象點P,且所有從S到P的光程都相等(光程長度用光波長量度)。儘管通過透鏡中心的光線的幾何長度比從S到P的其它光線的長度都短,但因為透鏡中心較厚,故各光程的波長數是相等的。因為透鏡的折射率較高,所以光波在透鏡中的傳播比在空氣中要慢。
除了對摺射光線作幾何追跡外,也要考慮衍射存在,此時,透鏡可視為一圓形開孔,該開孔在遠場條件下產生衍射,其結果是在P和P'點所成的象不很清晰,圍繞該兩點各有一個遠場的圓形衍射斑,因此,當兩個物點靠得很近時,物點的象就疊加在一起,因此要問:物體靠得多近尚能被分辨?
瑞利判據指出,兩個等亮度的物點,如果其中之一的象的衍射斑中央最大正好落在另一衍射斑的第一個最小上,即其暗環上,則說這兩個物點能被光學系統的鏡頭所分辨。換句話說,兩個衍射圖樣中心的距離應該等於中心亮斑的半徑。
現再看上圖,其中象點P和P‘的輻照度曲線表示在右邊,最小可分辨角間距可寫成
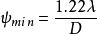 分辨極限
分辨極限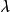 分辨極限
分辨極限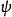 分辨極限
分辨極限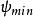 分辨極限
分辨極限其中D是開孔的直徑, 是光源的波長。因此,按瑞利判據,如果分辨角 小於 ,象就無法分辨。
顯微鏡的分辨極限
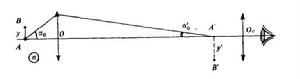 顯微鏡的分辨極限
顯微鏡的分辨極限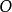 分辨極限
分辨極限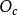 分辨極限
分辨極限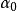 分辨極限
分辨極限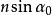 分辨極限
分辨極限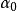 分辨極限
分辨極限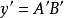 分辨極限
分辨極限兩個強度相同的光點A和B,它們位於用顯微鏡檢查的物平面上(如圖)。顯微鏡由物鏡(圓孔徑)和目鏡 組成.設 是A點對物鏡半徑所張的角,n是介質的折射率,乘積 是顯微鏡物鏡的數值孔徑。其實,顯微鏡的物鏡是由幾塊透鏡組成的,角 是A點對第一個透鏡(正面透鏡)的半徑所張的角。和前面一樣,A和B的像是中心A'和B'(A和B的幾何像)的兩個衍射斑點。如果這兩個斑點中心的距離 由(式表示:
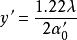 分辨極限
分辨極限則在分辨極限內.顯微鏡的物鏡總是滿足正弦條件(阿培條件),並可以寫成
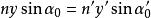 分辨極限
分辨極限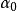 分辨極限
分辨極限其中y是物平面上兩點之間的距離AB,n'是像空間的折射率。在顯微鏡里,角總是小的,而且n'=1。因此有
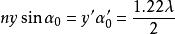 分辨極限
分辨極限 分辨極限
分辨極限由此得出 .
