定義
1967年,Mandelbrot在美國權威的《科學》雜誌上發表了題為《英國的海岸線有多長?統計自相似和分數維度》(How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension)的著名論文。海岸線作為曲線,其特徵是極不規則、極不光滑的,呈現極其蜿蜒複雜的變化。我們不能從形狀和結構上區分這部分海岸與那部分海岸有什麼本質的不同,這種幾乎同樣程度的不規則性和複雜性,說明海岸線在形貌上是自相似的,也就是局部形態和整體態的相似。在沒有建築物或其他東西作為參照物時,在空中拍攝的100公里長的海岸線與放大了的10公里長海岸線的兩張照片,看上去會十分相似。事實上,具有自相似性的形態廣泛存在於自然界中,如:連綿的山川、飄浮的雲朵、岩石的斷裂口、粒子的布朗運動、樹冠、花菜、大腦皮層……Mandelbrot把這些部分與整體以某種方式相似的形體稱為分形(fractal)。1975年,他創立了分形幾何學(Fractal Geometry)。在此基礎上,形成了研究分形性質及其套用的科學,稱為分形理論。
原則
線性分形又稱為自相似分形。自相似原則和疊代生成原則是分形理論的重要原則。它表征分形在通常的幾何變換下具有不變性,即標度無關性。由自相似性是從不同尺度的對稱出發,也就意味著遞歸。分形形體中的自相似性可以是完全相同,也可以是統計意義上的相似。標準的自相似分形是數學上的抽象,疊代生成無限精細的結構,如科赫曲線(Koch snowflake)、謝爾賓斯基地毯(Sierpinski carpet)等。這種有規分形只是少數,絕大部分分形是統計意義上的無規分形。
這裡再進一步介紹分形的分類,根據自相似性的程度,分形可以分為 有規分形和 無規分形,有規分形是指具體有嚴格的自相似性,即可以通過簡單的數學模型來描述其相似性的分形,比如三分康托集、Koch曲線等;無規分形是指具有統計學意義上的自相似性的分形,比如曲折連綿的海岸線,漂浮的雲朵等。
分形模型
cantor(康托)三分集
 三分康托集的構造過程
三分康托集的構造過程1883年,德國數學家康托(G.Cantor)提出了如今廣為人知的三分康托集,或稱康托爾集。三分康托集是很容易構造的,然而,它卻顯示出許多最典型的分形特徵。它是從單位區間出發,再由這個區間不斷地去掉部分子區間的過程構造出來的(如右圖)。其詳細構造過程是:第一步,把閉區間[0,1]平均分為三段,去掉中間的 1/3 部分段,則只剩下兩個閉區間[0,1/3]和[2/3,1]。第二步,再將剩下的兩個閉區間各自平均分為三段,同樣去掉中間的區間段,這時剩下四段閉區間:[0,1/9],[2/9,1/3],[2/3,7/9]和[8/9,1]。第三步,重複刪除每個小區間中間的 1/3 段。如此不斷的分割下去, 最後剩下的各個小區間段就構成了三分康托集。 三分康托集的豪斯多夫維是0.6309。
Koch 曲線
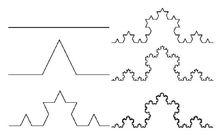 Koch 曲線的生成過程
Koch 曲線的生成過程1904年,瑞典數學家柯赫構造了 “Koch曲線”幾何圖形。Koch曲線大於一維,具有無限的長度,但是又小於二維。它和三分康托集一樣,是一個典型的分形。根據分形的次數不同,生成的Koch 曲線也有很多種,比如三次 Koch 曲線,四次 Koch 曲線等。下面以三次 Koch 曲線為例,介紹 Koch 曲線的構造方法,其它的可依此類推。三次Koch曲線的構造過程主要分為三大步驟:第一步,給定一個初始圖形——一條線段;第二步,將這條線段中間的 1/3 處向外折起;第三步,按照第二步的方法不斷的把各段線段中間的 1/3 處向外折起。這樣無限的進行下去,最終即可構造出Koch曲線。其圖例構造過程如右圖所示(疊代了 5 次的圖形)。
Julia 集
 Julia 集
Julia 集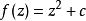 分形理論
分形理論Julia 集是由法國數學家 Gaston Julia 和 Pierre Faton 在發展了複變函數疊代的基礎理論後獲得的。Julia 集也是一個典型的分形,只是在表達上相當複雜,難以用古典的數學方法描述。朱利亞集合由一個複變函數生成,其中c為常數。
儘管這個複變函數看起來很簡單,然而它卻能夠生成很複雜的分形圖形。
右圖為朱利亞集合生成的圖形,由於c可以是任意值,所以當c取不同的值時,制出的圖形也不相同。
分維作用
分維,又稱分形維或分數維,作為分形的定量表征和基本參數,是分形理論的又一重要原則。長期以來人們習慣於將點定義為零維,直線為一維,平面為二維,空間為三維,愛因斯坦在相對論中引入時間維,就形成四維時空。對某一問題給予多方面的考慮,可建立高維空間,但都是整數維。在數學上,把歐氏空間的幾何對象連續地拉伸、壓縮、扭曲,維數也不變,這就是拓撲維數。然而,這種傳統的維數觀受到了挑戰。曼德布羅特曾描述過一個繩球的維數:從很遠的距離觀察這個繩球,可看作一點(零維);從較近的距離觀察,它充滿了一個球形空間(三維);再近一些,就看到了繩子(一維);再向微觀深入,繩子又變成了三維的柱,三維的柱又可分解成一維的纖維。那么,介於這些觀察點之間的中間狀態又如何呢?
顯然,並沒有繩球從三維對象變成一維對象的確切界限。數學家豪斯道夫(Hausdorff)在1919年提出了連續空間的概念,也就是空間維數是可以連續變化的,它可以是自然數,也可以是正有理數或正無理數,稱為豪斯道夫維數。記作Df,一般的表達式為:K=L^Df,也作K=(1/L)^(-Df),取自然對數並整理得Df=lnK/lnL,其中L為某客體沿其每個獨立方向皆擴大的倍數,K為得到的新客體是原客體的倍數。Df在一般情況下不一定是自然數。因此,曼德布羅特也把分形定義為豪斯道夫維數大於或等於拓撲維數的集合。英國的海岸線為什麼測不準?因為歐氏一維測度與海岸線的維數不一致。根據曼德布羅特的計算,英國海岸線的維數為1.26。有了分維,海岸線的長度就確定了。
意義
上世紀80年代初開始的“分形熱”經久不息。分形作為一種新的概念和方法,正在許多領域開展套用探索。美國物理學大師約翰·惠勒說過:今後誰不熟悉分形,誰就不能被稱為科學上的文化人。由此可見分形的重要性。 中國著名學者周海中教授認為:分形幾何不僅展示了數學之美,也揭示了世界的本質,還改變了人們理解自然奧秘的方式;可以說分形幾何是真正描述大自然的幾何學,對它的研究也極大地拓展了人類的認知疆域。 分形幾何學作為當今世界十分風靡和活躍的新理論、新學科,它的出現,使人們重新審視這個世界:世界是非線性的,分形無處不在。分形幾何學不僅讓人們感悟到科學與藝術的融合,數學與藝術審美的統一,而且還有其深刻的科學方法論意義。
註:分形理論好比拿著顯微鏡看一公里有多長只適用於科學研究,對於學習和現實生活中的長度,我們所採用的依然是理想情況下的約定俗成。

