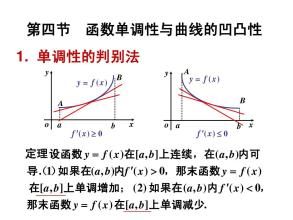
幾何定義
 函式的凹凸性
函式的凹凸性在函式f(x)的圖象上取任意兩點,如果函式圖象在這兩點之間的部分總在連線這兩點的線段的下方,那么這個函式就是凹函式。
直觀上看,凸函式就是圖象向上突出來的。比如
如果函式f(x)在區間I上二階可導,則f(x)在區間I上是凹函式的充要條件是f''(x)>=0;f(x)在區間I上是凸函式的充要條件是f''(x)<=0;
拐點:曲線上有切線的凹凸分界點
不同說法
不過補充一下,中國數學界關於函式凹凸性定義和國外很多定義是反的。ConvexFunction在國內的數學書中指凹函式。ConcaveFunction指凸函式。在國內涉及經濟學的很多書中,凹凸性的提法和國外的提法是一致的,也就是和單純的數學教材是反的。很頭大的問題。
另外,國內各不同學科教材、輔導書的關於凹凸的說法也是相反的。一般來說,可按如下方法準確說明:
1、f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),即V型,為“凸向原點”,或“下凸”(也可說上凹),(有的簡稱凸有的簡稱凹)
2、f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),即A型,為“凹向原點”,或“上凸”(下凹),(同樣有的簡稱凹有的簡稱凸)
凸/凹向原點這種說法一目了然。上下凸的說法也沒有歧義。
在二維環境下,就是通常所說的平面直角坐標系中,可以通過畫圖直觀地看出一條二維曲線是凸還是凹,當然它也對應一個解析表示形式,就是那個不等式。但是,在多維情況下,圖形是畫不出來的,這就沒法從直觀上理解“凹”和“凸“的含義了,只能通過表達式,當然n維的表達式比二維的肯定要複雜,但是,不管是從圖形上直觀理解還是從表達式上理解,都是描述的同一個客觀事實。而且,按照函式圖形來定義的凹凸和按照函式來定義的凹凸正好相反。
不等式
琴生(Jensen)不等式(也稱為詹森不等式):(注意前提、等號成立條件)設f(x)為凸函式,則f[(x1+x2+……+xn)/n]≤[f(x1)+f(x2)+……+f(xn)]/n(下凸);設f(x)為凹函式,f[(x1+x2+……+xn)/n]≥[f(x1)+f(x2)+……+f(xn)]/n(上凸),稱為琴生不等式。
加權形式為:f[(a1*x1+a2*x2+……+an*xn)]≤a1f(x1)+a2f(x2)+……+anf(xn)(下凸);f[(a1*x1+a2*x2+……+an*xn)]≥a1f(x1)+a2f(x2)+……+anf(xn)(上凸),其中ai≥0(i=1,2,……,n),且a1+a2+……+an=1.