定義
在數理統計學中, 似然函式是一種關於統計模型中的參數的函式,表示模型參數中的 似然性。
給定輸出x時,關於參數θ的似然函式L(θ|x)(在數值上)等於給定參數θ後變數X的機率:
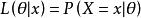 似然函式
似然函式似然函式在推斷統計學(Statistical inference)中扮演重要角色,如在最大似然估計和費雪信息之中的套用等等。“似然性”與“或然性”或“機率”意思相近,都是指某種事件發生的可能性,但是在統計學中,“似然性”和“或然性”或“機率”又有明確的區分。機率用於在已知一些參數的情況下,預測接下來的觀測所得到的結果,而似然性則是用於在已知某些觀測所得到的結果時,對有關事物的性質的參數進行估計。
分布類型
離散型機率分布
假定一個關於參數θ、具有離散型機率分布P的隨機變數X,則在給定X的輸出x時,參數θ的似然函式可表示為
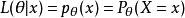 似然函式
似然函式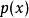 似然函式
似然函式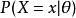 似然函式
似然函式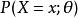 似然函式
似然函式其中, 表示X取x時的機率。上式常常寫為 或者 。需要注意的是,此處並非條件機率,因為θ不(總)是隨機變數。
連續型機率分布
假定一個關於參數θ、具有連續機率密度函式f的隨機變數X,則在給定X的輸出x時,參數θ的似然函式可表示為
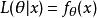 似然函式
似然函式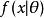 似然函式
似然函式上式常常寫為 ,同樣需要注意的是,此處並非條件機率密度函式。
似然函式的主要用法在於比較它相對取值,雖然這個數值本身不具備任何含義。例如,考慮一組樣本,當其輸出固定時,這組樣本的某個未知參數往往會傾向於等於某個特定值,而不是隨便的其他數,此時,似然函式是最大化的。
似然函式乘以一個正的常數之後仍然是似然函式,其取值並不需要滿足歸一化條件
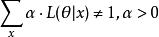 似然函式
似然函式似然函式的這種特性還允許我們疊加計算一組具備相同含義的參數的獨立同分布樣本的似然函式。
關於利用似然函式進行統計推斷的套用,可以參考最大似然估計(Maximum likelihood estimation)方法和似然比檢驗(Likelihood-ratio testing)方法。
對數似然函式
涉及到似然函式的許多套用中,更方便的是使用似然函式的自然對數形式,即“對數似然函式”。求解一個函式的極大化往往需要求解該函式的關於未知參數的偏導數。由於對數函式是單調遞增的,而且對數似然函式在極大化求解時較為方便,所以對數似然函式常用在最大似然估計及相關領域中。例如:求解Gamma分布中參數的最大似然估計問題:
 似然函式
似然函式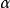 似然函式
似然函式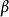 似然函式
似然函式假定服從Gamma分布的隨機變數 具有兩個參數 和 ,考慮如下似然函式
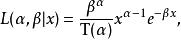 似然函式
似然函式 似然函式
似然函式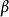 似然函式
似然函式如果想從輸出 中估計參數 ,直接求解上式的極大化未免有些難度。在取對數似然函式後,
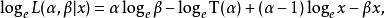 似然函式
似然函式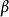 似然函式
似然函式再取關於 的偏導數等於0的解,
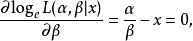 似然函式
似然函式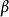 似然函式
似然函式最終獲得 的最大似然估計
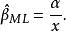 似然函式
似然函式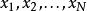 似然函式
似然函式當存在一組獨立同分布的樣本 時,
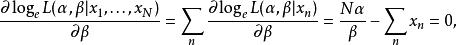 似然函式
似然函式故而
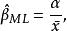 似然函式
似然函式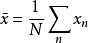 似然函式
似然函式其中, 。
參數化模型的似然函式
 似然函式
似然函式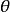 似然函式
似然函式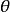 似然函式
似然函式有時我們需要考慮在給定一組樣本輸出 時,使用待估參數 的假設值與其真實值之間的誤差,此時似然函式變成是關於待估參數 的函式。
計算實例
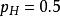 似然函式
似然函式考慮投擲一枚硬幣的實驗。假如已知投出的硬幣正面朝上的機率是 ,便可以知道投擲若干次後出現各種結果的可能性。比如說,投兩次都是正面朝上的機率是0.25:
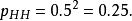 似然函式
似然函式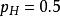 似然函式
似然函式從另一個角度上說,給定“投兩次都是正面朝上”的觀測,則硬幣正面朝上的機率為0.5的似然是
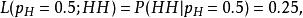 似然函式
似然函式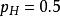 似然函式
似然函式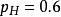 似然函式
似然函式儘管這並不表示當觀測到兩次正面朝上時 的“機率”是0.25。如果考慮 ,那么似然函式的值會變大
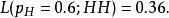 似然函式
似然函式這說明,如果參數的取值變成0.6的話,結果觀測到連續兩次正面朝上的機率要比假設0.5 時更大。也就是說,參數取成0.6 要比取成0.5 更有說服力,更為“合理”。總之,似然函式的重要性不是它的具體取值,而是當參數變化時函式到底變小還是變大。對同一個似然函式,如果存在一個參數值,使得它的函式值達到最大的話,那么這個值就是最為“合理”的參數值。
套用
最大似然估計
最大似然估計是似然函式最初也是最自然的套用。上文已經提到,似然函式取得最大值表示相應的參數能夠使得統計模型最為合理。從這樣一個想法出發,最大似然估計的做法是:首先選取似然函式(一般是機率密度函式或機率質量函式),整理之後求最大值。實際套用中一般會取似然函式的對數作為求最大值的函式,這樣求出的最大值和直接求最大值得到的結果是相同的。似然函式的最大值不一定唯一,也不一定存在。與矩法估計比較,最大似然估計的精確度較高,信息損失較少,但計算量較大。
給定一個機率分布D,假定其機率密度函式(連續分布)或機率聚集函式(離散分布)為 f,以及一個分布參數θ,我們可以從這個分布中抽出一個具有 n個值的採樣 X, X,..., X,通過利用 f,我們就能計算出其機率:
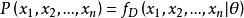 似然函式
似然函式但是,我們可能不知道θ的值,儘管我們知道這些採樣數據來自於分布D。那么我們如何才能估計出θ呢?一個自然的想法是從這個分布中抽出一個具有 n個值的採樣X,X,...,X,然後用這些採樣數據來估計θ。
一旦我們獲得X,X,...,X,我們就能從中找到一個關於θ的估計。最大似然估計會尋找關於 θ的最可能的值(即,在所有可能的θ取值中,尋找一個值使這個採樣的“可能性”最大化)。這種方法正好同一些其他的估計方法不同,如θ的非偏估計,非偏估計未必會輸出一個最可能的值,而是會輸出一個既不高估也不低估的θ值。
要在數學上實現最大似然估計法,我們首先要定義可能性:
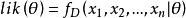 似然函式
似然函式並且在θ的所有取值上,使這個函式最大化。這個使可能性最大的值即被稱為θ的 最大似然估計。
似然比檢驗
似然比檢驗是利用似然函式來檢測某個假設(或限制)是否有效的一種檢驗。一般情況下,要檢測某個附加的參數限制是否是正確的,可以將加入附加限制條件的較複雜模型的似然函式最大值與之前的較簡單模型的似然函式最大值進行比較。如果參數限制是正確的,那么加入這樣一個參數應當不會造成似然函式最大值的大幅變動。一般使用兩者的比例來進行比較,這個比值是卡方分配。
尼曼-皮爾森引理說明,似然比檢驗是所有具有同等顯著性差異的檢驗中最有統計效力的檢驗。
似然比檢驗是一種尋求檢驗方法的一般法則。其基本思想如下: 設由n個觀察值X1,X2,…,Xn組成的隨機樣本來自密度函式為f(X; θ)的總體,其中θ為未知參數。要檢驗的無效假設是H: θ=θ,備擇假設是H1:θ≠θ檢驗水準為α。為此,求似然函式在θ=θ處的值與在θ=θ(極大點)處的值(即極大值)之比,記作λ,可以知道:
(1) 兩似然函式值之比值λ只是樣本觀察值的函式,不包含任何未知參數。
(2) 0≤λ≤1,因為似然函式值不會為負,且λ的分母為似然函式的極大值,不會小於分子。
(3)越接近θ時,λ越大;反之,與θ相差愈大,λ愈小。因此,若能由給定的α求得顯著性界值λ,則可按以下規則進行統計推斷:
當λ≤λ,拒絕H,接受H;當λ>λ,不拒絕H,
這裡 P(λ≤λ)=α。(2)對於離散型的隨機變數,只需把密度函式置換成機率函式p(X;θ),即
這一檢驗方法還可以推廣到有k個參數的情形。
但是,要確定λ的界值λ,必須知道當H成立時λ的分布。當不了解λ的分布或者它的分布太複雜時,就難於確定其界值λ,此時可利用下述統計原理: 當樣本含量n較大時,-2lnλ (本書中用符號G表示)近似x2分布;當自由度大於1,甚至n較小時,這種近似的程度也是相當滿意的。基於上述原理,統計中廣泛套用對數似然比檢驗,通過計算統計量G,可按x2分布處理,不但計算方便,而且只要自由度大於1,就不必考慮理論頻數大小的問題。關於似然比檢驗的具體套用,詳見條目“頻數分布的擬合優度”、“兩樣本率比較”、“多個樣本率比較”、“樣本構成比的比較”以及“計數資料的相關分析”等。

