定理簡介
素數定理描述素數的大致分布情況。
素數的出現規律一直困惑著數學家。一個個地看,素數在正整數中的出現沒有什麼規律。可是總體地看,素數的個數竟然有規可循。對正實數x,定義π(x)為不大於x的素數個數。數學家找到了一些函式來估計π(x)的增長。以下是第一個這樣的估計。 π(x)≈x/ln x 其中ln x為x的自然對數。上式的意思是當x趨近∞,π(x) 和x/ln x的比趨 近1(註:該結果為高斯所發現)。但這不表示它們的數值隨著x增大而接近。 下面是對π(x)更好的估計: π(x)=Li (x) + O (x e^(-(ln x)^(1/2)/15),當 x 趨近∞。 其中 Li(x) = ∫(dt/ln x2,x),而關係式右邊第二項是誤差估計,詳見大O符號。 下表比較了π(x),x/ln x和Li(x): x π(x) π(x) - x/ln(x) Li(x) - π(x) x/π(x)
素數定理可以給出第n個素數p(n)的漸近估計: :p(n)~n/ln n. 它也給出從整數中抽到素數的機率。從不大於n的自然數隨機選一個,它是素數的機率大約是1/ln n。 這定理的式子於1798年法國數學家勒讓德提出。1896年法國數學家哈達瑪(JacquesHadamard)和比利時數學家普森(Charles Jean de la Vallée-Poussin)先後獨立給出證明。證明用到了複分析,尤其是黎曼ζ函式。 因為黎曼ζ函式與π(x)關係密切,關於黎曼ζ函式的黎曼猜想對數論很重要。一旦猜想獲證,便能大大改進素數定理誤差的估計。1901年瑞典數學家Helge von Koch證明出,假設黎曼猜想成立,以上關係式誤差項的估計可改進為 :π(x)=Li (x) + O (x^(1/2) ln x) 至於大O項的常數則還未知道。
初等證明
素數定理有些初等證明只需用數論的方法。第一個初等證明於1949年由匈牙利數學家保羅·艾狄胥(“愛爾多斯”,或“愛爾多希”)和挪威數學家阿特利·西爾伯格合作得出。 在此之前一些數學家不相信能找出不需藉助艱深數學的初等證明。像英國數學家哈代便說過素數定理必須以複分析證明,顯出定理結果的「深度」。他認為只用到實數不足以解決某些問題,必須引進複數來解決。這是憑感覺說出來的,覺得一些方法比別的更高等也更厲害,而素數定理的初等證明動搖了這論調。Selberg-艾狄胥的證明正好表示,看似初等的組合數學,威力也可以很大。 但是,有必要指出的是,雖然該初等證明只用到初等的辦法,其難度甚至要比用到複分析的證明遠為困難。
素數簡介
概念
質數又稱素數。指在一個大於1的自然數中,除了1和此整數自身外,不能被其他自然數整除的數。質數是與合數相對立的兩個概念,二者構成了數論當中最基礎的定義之一。基於質數定義的基礎之上而建立的問題有很多世界級的難題,如哥德巴赫猜想等。截至2018年2月底,質數尚未完全找到通項公式。
通項公式
 素數公式
素數公式n的點集分兩組,一組為偽素數的變數集,一組為素數的變數集合,其中偽素數的變數集合有以下方程式來確定:
素數變數n(x,y)的充分必要條件為:
n(x,y)為偶數時:
1.n(x,y)為偶數時:
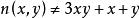 素數公式
素數公式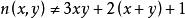 素數公式
素數公式2.n(x,y)為奇數時:
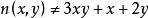 素數公式
素數公式滿足以上方程則為素數的變數,但方程不包括2,3這兩個素數。
偽素數變數n(x,y)的充分必要條件為:
n(x,y)為偶數時:
1.n(x,y)為偶數時:
 素數公式
素數公式 素數公式
素數公式2.n(x,y)為奇數時:
 素數公式
素數公式密度公式
 素數公式
素數公式根據 :
 素數公式
素數公式構造一函式如下:
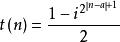 素數公式
素數公式1-1
 素數公式
素數公式其中a為常數 且
 素數公式
素數公式根據1-1性質 以多項式
 素數公式
素數公式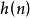 素數公式
素數公式為中的指數,結合公式1-1
得素數密度公式:
 素數公式
素數公式 素數公式
素數公式此公式中定義1為素數
質數的無窮性的證明
質數的個數是無窮的。最經典的證明由歐幾里得證得,在他的《幾何原本》中就有記載。它使用了現在證明常用的方法:反證法。具體的證明如下:
●假設質數只有有限的n個,從小到大依次排列為p1,p2,……,pn,設 N = p1 × p2 × …… × pn,那么,N+1是素數或者不是素數。
●如果N+1為素數,則N+1要大於p1,p2,……,pn,所以它不在那些假設的素數集合中。
●如果N+1為合數,因為任何一個合數都可以分解為幾個素數的積;而N和N+1的最大公約數是1,所以N+1不可能被p1,p2,……,pn整除,所以該合數分解得到的素因數肯定不在假設的素數集合中。
●因此無論該數是素數還是合數,都意味著在假設的有限個素數之外還存在著其他素數。
●對任何有限個素數的集合來說,用上述的方法永遠可以得到有一個素數不在假設的素數集合中的結論。
●所以原先的假設不成立。也就是說,素數有無窮多個。
其他數學家也給出了他們自己的證明。歐拉利用黎曼ζ函式證明了全部素數的倒數之和是發散的,恩斯特·庫默的證明更為簡潔,Hillel Furstenberg則用拓撲學加以了證明。
對於一定範圍內的素數數目的計算
儘管整個素數是無窮的,仍然有人會問“100000以下有多少個素數?”,“一個隨機的100位數多大可能是素數?”。素數定理可以回答此問題。
素數輸出及個數計算
利用excel宏能夠精確計算每個周期內的素數總數,不過不含2,3的數量。以下程式在excel 2003能夠計算361個周期以內的素數。運行前必須在單元格O1輸入不大於361的自然數,周期數361,運行需要約16分鐘,小周期內運行很快,程式中ws(a,b)就是偽素數的變數函式,N為周期,程式運行結束後單元格Q1為全部統計素數總數,R1~W1為各列素數數量,如果想計算周期大於361時,必須修改以下程式,本程式已經最佳化,比任何篩選程式運行都要快,以下是本程式代碼:
Sub 求素數()
Dim N As Long, R As Long, J As Long, I As Long, k As Long, Y As Long, y1 As Long
Dim S1 As String, S As String
N = Range("O1") '程式運行前請在表格O1輸入不大於361的周期數
For Y = 1 To WS(N, N) Step 1
If WS(Y, 2) <= WS(N, N) Then
R = Y
End If
Next
Range("A1:N65536") = ""
Range("P1:X1") = ""
Range("P1") = "變數為" & WS(N, N) & "以內素數合計"
Range("A1") = 5
For k = 1 To WS(N, N) Step 1
y1 = (k - 3 + 2 * (Sin(3.14159265358979 * k / 2)) ^ 2)
If y1 Mod 5 = 0 Then
k = k + 1
Else
k = k
End If
If k <= 65536 Then
S1 = "A" & k
ElseIf k > 65536 And k <= 65536 * 2 Then
S1 = "B" & k - 65536
ElseIf k > 65536 * 2 And k <= 65536 * 3 Then
S1 = "C" & k - 65536 * 2
ElseIf k > 65536 * 3 And k <= 65536 * 4 Then
S1 = "D" & k - 65536 * 3
ElseIf k > 65536 * 4 And k <= 65536 * 5 Then
S1 = "E" & k - 65536 * 4
ElseIf k > 65536 * 5 And k <= 65536 * 6 Then
S1 = "F" & k - 65536 * 5
End If
Range(S1) = 3 * k + 1 + (Sin(3.14159265358979 * k / 2)) ^ 2
Next
For I = 1 To N Step 1
For J = 1 To R Step 1
If WSF(J, I, N) > 0 And WSF(J, I, N) <= WS(N, N) Then
If WSF(J, I, N) <= 65536 Then
S = "A" & WSF(J, I, N)
ElseIf WSF(J, I, N) > 65536 And WSF(J, I, N) <= 65536 * 2 Then
S = "B" & WSF(J, I, N) - 65536
ElseIf WSF(J, I, N) > 65536 * 2 And WSF(J, I, N) <= 65536 * 3 Then
S = "C" & WSF(J, I, R) - 65536 * 2
ElseIf WSF(J, I, N) > 65536 * 3 And WSF(J, I, N) <= 65536 * 4 Then
S = "D" & WSF(J, I, N) - 65536 * 3
ElseIf WSF(J, I, N) > 65536 * 4 And WSF(J, I, N) <= 65536 * 5 Then
S = "E" & WSF(J, I, N) - 65536 * 4
ElseIf WSF(J, I, N) > 65536 * 5 And WSF(J, I, N) <= 65536 * 6 Then
S = "F" & WSF(J, I, N) - 65536 * 5
End If
If WSF(J, I, N) > 0 Then
S = S
Range(S) = ""
Else
S = ""
End If
End If
Next
If I >= N Then
Call MR
End If
Next
End Sub
Sub MR()
Columns("A:A").Select
Selection.Sort Key1:=Range("A1"), Order1:=xlAscending, Header:=xlGuess, _
OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, SortMethod _
:=xlPinYin, DataOption1:=xlSortNormal
Columns("B:B").Select
Selection.Sort Key1:=Range("B1"), Order1:=xlAscending, Header:=xlGuess, _
OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, SortMethod _
:=xlPinYin, DataOption1:=xlSortNormal
Columns("C:C").Select
Selection.Sort Key1:=Range("C1"), Order1:=xlAscending, Header:=xlGuess, _
OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, SortMethod _
:=xlPinYin, DataOption1:=xlSortNormal
Columns("D:D").Select
Selection.Sort Key1:=Range("D1"), Order1:=xlAscending, Header:=xlGuess, _
OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, SortMethod _
:=xlPinYin, DataOption1:=xlSortNormal
Columns("E:E").Select
Selection.Sort Key1:=Range("E1"), Order1:=xlAscending, Header:=xlGuess, _
OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, SortMethod _
:=xlPinYin, DataOption1:=xlSortNormal
Columns("F:F").Select
Selection.Sort Key1:=Range("F1"), Order1:=xlAscending, Header:=xlGuess, _
OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, SortMethod _
:=xlPinYin, DataOption1:=xlSortNormal
Range("Q1").FormulaR1C1 = "=COUNTIF(C[-16]:C[-11],"">0"")"
Range("R1").FormulaR1C1 = "=COUNTIF(C[-17],"">0"")"
Range("S1").FormulaR1C1 = "=COUNTIF(C[-17],"">0"")"
Range("T1").FormulaR1C1 = "=COUNTIF(C[-17],"">0"")"
Range("U1").FormulaR1C1 = "=COUNTIF(C[-17],"">0"")"
Range("V1").FormulaR1C1 = "=COUNTIF(C[-17],"">0"")"
Range("W1").FormulaR1C1 = "=COUNTIF(C[-17],"">0"")"
End Sub
Function WS(A As Variant, B As Variant) As Variant
If A Mod 2 = 1 And B Mod 2 = 1 Then
WS = 3 * A * B + 2 * (A + B) + 1
End If
If A Mod 2 = 0 And B Mod 2 = 0 Then
WS = 3 * A * B + (A + B)
End If
If A Mod 2 = 1 And B Mod 2 = 0 Then
WS = 3 * A * B + A + 2 * B
End If
If A Mod 2 = 0 And B Mod 2 = 1 Then
WS = 3 * A * B + B + 2 * A
End If
WS = WS
If A < B Then
WS = 0
Else
WS = WS
End If
WS = WS
End Function
Function WSF(A As Variant, B As Variant, N As Long) As Variant
Dim d As Variant
d = WS(A, B) - 3 + 2 * (Sin(3.14159265358979 * WS(A, B) / 2)) ^ 2
If WS(A, B) <= WS(N, N) And d Mod 5 <> 0 Then
WSF = WS(A, B)
Else
WSF = 0
End If
End Function
素數逼近函式
 素數公式
素數公式逼近函式其實是中值函式,實際素數方程值減去逼近函式,得到素數的余函式εx,圖象如下:
檢驗素數
檢查一個正整數N是否為素數,最簡單的方法就是試除法,將該數N用小於等於根號N的所有素數去試除,若均無法整除,N則為素數,參見素數判定法則。
2002年,印度人M. Agrawal、N. Kayal以及N. Saxena提出了AKS質數測試算法,證明了可以在多項式時間內檢驗是否為素數。
趣味數學
| 趣味數學以帶有強烈的遊戲色彩知名於世。歐拉就是通過對bridge-crossing之謎的分析打下了拓撲學的基礎。萊布尼茨也寫到過他在獨自玩插棍遊戲時分析問題的樂趣。希爾伯特證明了切割幾何圖形中的許多重要定理。馮·紐曼奠基了博弈論。最受大眾歡迎的計算機遊戲—生命是英國著名數學家康威發明的。愛因斯坦也收藏了整整一書架關於數學遊戲和數學謎的書。 |
