解釋
若n能整除2^(n-1)-1,並n是非偶數的合數,那么n就是偽素數。
例子
2^(5-1)-1=15,15|5. 2^(3-1)-1=3,3|3.但很多都是素數,如3,5,7,29,31……
1919年數學家薩魯斯找到了反例:2^(341-1)-1|341,而341=11*31是合數,341就成了第一個偽素數。以後又發現了許多偽素數:561 645 1105 1387 1729……
起源
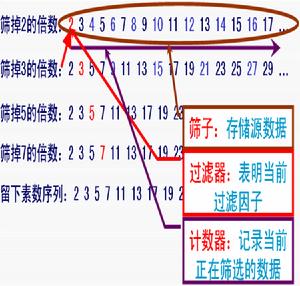 偽素數
偽素數如果p是一個素數,且a不能被p整除,則ap-1-1能被P整除(等價的說法是ap-a能被素數p整除)。
後人稱這個定理為費馬小定理,以和費馬大定理相區別。費馬小定理奠定了現代數論中素數判定的基礎。
按費馬小定理,如果一個奇數n不能整除2n-2,則n必為合數(這是費馬小定理的一個逆否命題)。但是,如果奇數n>1能整除2n-2, n就一定是素數嗎?就是說,費馬小定理的逆命題是否成立?對於1<n<300的數來說,計算可知,能整除2n-2的奇數n都是素數,這使得人們在很長的時間內認為費馬小定理的逆命題當然成立。德國數學家萊布尼茨曾在1680年6月和1681年12月兩次宣布他證明了這樣一個命題:如果n不是素數,則2n-2不能被n整除(這是下述命題的逆否命題:如果2n-2能被n整除,則n是素數),但沒發表他的證明。1742年4月,德國數學家哥德巴赫在給歐拉的信中表示要證明費馬小定理的逆定理,但似乎也無結果。
1819年,法國數學家沙路斯發現,雖然341整除2341-2,但341是合數,341=11×31。這一反例表明費馬小定理的逆定理不成立。1830年,一位匿名德國數學家指出更一般的構造反例的方法,他指出,只要能找到兩個奇素數p和q,使它們的積pq能同時整除2p-1-1與2q-1-1,那么就可得到pq整除2pq-1-1。按此方法,人們發現除341外,還有561,645,1105,1389,1729,1905等也具有上述性質。於是,人們把能整除2n一2的合數n稱為偽素數。1926年,普列特製成5000萬以內的偽素數表,1938年他又推進上限到1億,為此,有時偽素數亦被稱為普列特數。
提出偽素數後自然就產生了類似素數的問題,並得到人們的研究。如偽素數有多少個?人們指出,偽素數有無窮多,1903年麥洛用一個構造性方法對此加以證明。他證明了,若n是奇偽素數,那么,n = 2n-1-1也是奇偽素數,我們已知有奇偽素數n0=341,按此法就可以構造出無窮多的奇偽素數來。再如是否存在偶偽素數?1950年,美國數學家D.H.萊默爾找到了第一個偶偽素數161038,161038=2×73×1103,73 |(2161038-2),1103 |(216038-2) 。1951年,荷蘭的畢格爾又找到了一個偶偽素數,並證明了存在無窮多個偶偽素數。
後來人們針對費馬小定理的一般情況,把偽素數概念一般化,就得出前面的定義。1904年,義大利數學家奇波拉給出一種構造a-偽素數的方法:
對於已知的整數a≥2,取p是任一奇素數,使p不能整除a(a2一1),則n=(a2p-1)/(a2-1)是a-偽素數。
他同時也證明了存在無窮多的一般偽素數。當然,在一般偽素數研究中,也有許多未解決的問題。例如,1952年杜帕克提出的,能否存在無窮多個偽素數,它們同時以2和3為底,或更一般些,能否存在無窮多個偽素數,它們同時以兩個不同的整數a與b為底(a≥2,b≥2,且a與b不是同一個整數的冪)。
偽素數的一個用途是利用偽素數表來判定一個奇數n是否為素數,這是D.H.萊默爾提出來的:如果n不能整除2n-1-1,則據費馬小定理知,n必為合數;如果n能整除2n-1-1,且n在偽素數表中,則n為合數,否則為素數。這種方法的關鍵就在於按偽素數表去掉偽素數,而這要求偽素數在能整除2n-1-1的數中相當少才行,這就是當n整除2n-1-1時,n是合數的比例問題。在前10億個自然數中,共有50847534個素數,而只有以2為底的偽素數5597個,即在此範圍內n整除2n-1-1產生合數的可能性只有0.011%。所以人們把整除2n-1-1的正整數n(>1)稱為殆素數。在10億之內,n整除2n-1-1同時整除3n-1-1的合數n只有1272個,即此時產生合數的可能性只有0.0025%。
如果存在合數n,對任何a>1,只要(a,n)=1時,n能整除an-1-1,則n被稱為卡邁克爾數。這種數是由美國數學家R.D.卡麥可於1912年提出來的。最小的卡麥可數為561,這種數在自然數中更少了,在10億之內,只有646個。一個問題就是:卡麥可數是否有無窮多?
解謎
享有"業餘數學之王"稱號的費馬曾經證明:若p為素數,則ap-a是p的倍數,進一步如果p與a互素,則顯然ap-1-1是p的倍數,用同餘式來表達就是:
ap-1=1 mod p
這個表達式無疑是數論大廈的一塊基石.對如此美妙的定理如果毫不動心,那他一定是只剩下一口氣的行屍走肉.推導這個公式用同餘式最方便,由於與素數p互素的數有p-1個,它們是:
1,2,3,...p-1
顯然有: a*2a*3a...a(p-1)=1*2*3...(p-1) mod p
即: ap-1*(p-1)!=(p-1)! mod p
兩邊同除以(p-1)!得到:
ap-1=1 mod p
再對a套用數學歸納法即可證明之.
但是它的逆定理是不成立的,即當ap-1-1能被p整除時,p不一定是素數,在1819年,法國數學家莎路斯首先發現,雖然341能夠整除2340-1,但是341=11*31為一個合數.後來有一位德國數學家一般性地證明了,只要找到兩個奇素數p,q,使得它們的積能同時整除2p-1-1,與2q-1-1,就能保證pq整除2pq-1-1.
偽素數有無窮多個,第一個證明這一點的是數學家邁羅在1903年給出的.如果n是偽素數,則2n-1也是偽素數,所以偽素數有無窮多個.除了上述的341之外,人們陸續發現了561,645,1105,1387,1729,1905等等.數學家普列特在1938年做出了1億以內的偽素數表.因此偽素數又叫做普列特數.
除了奇偽素數以外,竟然還有偶偽素數存在,美國著名數學家D.H.萊默在1950年找到了第一個偶偽素數:161038,後來荷蘭數學家畢格爾又發現了3個偶偽素數:215326,2568226和143742226,並且從理論上證明了存在無窮多個偶偽素數.
偽素數是針對底數為2的情形提出的.而對於一般的底數a,則提出了a-偽素數的概念,例如91能整除390-1,所以把91稱為3-偽素數.1904年,義大利數學家奇波拉給出了一種構造a-偽素數的方法:
對於已知的整數 a>=2,取任意奇素數 p,使得 p不能整除a(a2-1),則 n=(a2p-1)/(a2-1)必是a-偽素數.比如取 a=2,選 p=5,顯然 5不能整除2(22-1)=6,所以(210-1)/(22-1)=341 是偽素數.
對於已知的整數 a>=2,由於有無窮多個奇素數不能整除a(a2-1),所以a-偽素數有無窮多個.
利用偽素數表,數學家D.H.萊默建議按照如下程式來判別一個奇數是否是素數:如果p不能整除2p-1-1,則p必然為合數;如果p能整除2p-1-1,且p在偽素數表中,則p為合數,否則p為素數.顯然這是基於費馬小定理的檢驗法,我想如果再結合篩法,就會完全剔除這些偽素數.
畢竟偽素數比較稀少,在前10億個自然數中共有50847534個素數,而偽素數只有5597個,即大約只占萬分之一.而同時能以2,3為底的偽素數只有1272個,即大約5萬分之一.那么是否存在這樣的數p,它能夠整除所有的以2,3,4,...為底的費馬表達式,那么p一定是素數了吧?遺憾的是,竟然存在這樣的偽素數,它能夠整除以任何整數a為底(即使是負整數)的ap-1-1,561就是最小的一個例子:
a560-1=(a2)280-1=(a2-1)(...)=(a10-1)(...)=(a16-1)(...)
由於561=3*11*17,而由費馬小定理,3,11,17都能夠整除上式,所以561也能夠整除上式.這種極端的偽素數叫做絕對偽素數,又由於是首先由美國數學家卡麥可在1912年發現的,所以又叫做卡麥可數,為了判別什麼樣的整數是卡麥可數,他發現了一個準則:
如果整數n滿足如下條件
(1) n沒有平方因子,即n沒有相同的素因子;
(2) n是奇數且至少有3個不同的素數因子;
(3) 對於n的每一個素數因子p,p-1能夠整除n-1;
則 n 必為卡麥可數.反之,如果 n是卡麥可數,則 n必滿足上述3個條件.
1939年,數學家切尼克給出了一種構造卡麥可數的方法:
設m為自然數,且使得(6m+1),(12m+1),(18m+1)都是素數,則M3(m)=(6m+1)(12m+1)(18m+1)是具有3個素因子的卡麥可數.例如取m=1,則有M3(1)=7*13*19=1729是卡麥可數.類似地,自然數m是使得
Mk(m)=(6m+1)(12m+1)(9*2m+1)...(9*2k-2m+1) (k>=4)
中k個因子都是素數,則Mk(m)是含有k個素因子的卡麥可數.1985年,杜伯納得到了下面一些巨大的卡麥可數: m=5*7*11*13*...*397*882603*10185 時的含有3個素因子的卡麥可數M3(m)是一個1057位數,這是目前知道的最大的卡麥可數.其他的還有
m=323323*655899*1040/6 時的M4(m)是個207位數的卡麥可數.
m=323323*426135*1016/6 時的M5(m)是個139位數的卡麥可數.
m=323323*239556*107/6 時的M6(m)是個112位數的卡麥可數.
m=323323*160*8033 時的M7(m)是個93位數的卡麥可數.
1978年,約里納戈發現了8個卡麥可數,它們都具有13個素數因子.這是目前所知道的含有素數因子最多的一組卡麥可數.下表是目前所知道的小於x的以2為底的偽素數個數P(x)與卡麥可數的個數C(x)的分布情況.
x P(x) C(x)
1000 8 1
10000 22 7
100000 78 16
1000000 245 43
10000000 750 105
100000000 2057 255
1000000000 5597 646
10000000000 14887 1547
不超過100000的16個卡麥可數如下:
561,1105,1729,2465,2821,6601,8911,10585,15841,29341,41041,46657,52633,62745,63973,75361
留給人們的未解之謎是;
(1) 同時以a,b為底的偽素數是否有無窮多個?
(2) 卡麥可數是否有無窮多個?