漢字信息
拼音：huán
部首：王
部外筆畫：4
總筆畫：8
五筆86：GGI
五筆98：GDHY
倉頡：MGMF
筆順編號：11211324
四角號碼：11190
Unicode：CJK
統一漢字U+73AF
字形結構
漢字首尾分解:王不
漢字部件分解:王不
筆順編號:11211324
筆順讀寫:橫橫豎橫橫撇豎捺
基本字義
1.中央有孔的圓形佩玉：～佩。
2.圈形的東西：～形。連～。鐵～。花～。耳～。
3.圍繞：～視。～顧。～拜。～海。～球。～行（xíng）。日～食。
4.相互聯繫的許多事物中的一個：重要的一～。險象～生。
5.量詞，用於記錄射擊環靶的成績：今天打了十～。
6.姓。
詳細字義
〈名〉
1.形聲。從玉，瞏huán聲。本義：圓形而中間有孔的玉器。
2.同本義[jadebracelet]
環，璧也。——《說文》
肉好若一謂之不。——《爾雅·釋器》。李註：“其孔及邊肉大小適等。”
行步則有環佩之聲。——《禮記·經解》
孔子佩象環五寸。——《禮記·玉藻》
聞水聲，如鳴佩環。——唐·柳宗元《至小丘西小石潭記》
腰白玉之環。——明·宋濂《送東陽馬生序》[3]
3.又如：環佩（古人衣帶上所系的佩玉）；環玦（玉環和玉玦）；環琨（環與琨，並為玉佩）；環塡（兩種玉制的耳飾。環，耳環。塡，冠冕上的塞耳之玉）。
4.泛指圓圈形的物品[ring]
布巾環幅。——《儀禮·士喪禮》
瓜祭上環。——《禮記·玉藻》。註：“上環，頭忖也。”
5.又如：環中（圓環的中心；又比喻空虛而無是無非的境界）；環利通索（連環鐵索）。
6.數學中，具有加法和乘法運算的集合[ring]。其中任兩個元素的並與對稱差仍是該族中的元素。
7.化學中，環形的結構或多個原子的一種閉鏈[ring]。如：苯環；甾環。
〈動〉
1.環繞，圍繞[surround]
三江環之。——《國語·越語上》
戎翟之民實環之。——《國語·晉語二》
譬眾星之環極。——《文選·張衡·西京賦》
環而攻之。——《孟子·公孫丑下》
竹樹環合。——唐·柳宗元《至小丘西小石潭記》
賊環而進。——明·魏禧《大鐵椎傳》
環村皆獵戶。——清·徐珂《清稗類鈔·戰事類》
2.又如：環坐（環繞而坐）；環絛（束腰的絲帶）；環攻（圍攻）；環瞰（包圍窺伺）；環擊（圍攻）；環迫（四面威逼）。
3.鏇轉[revolve]
環拜以鐘鼓為節。——《周禮·樂師》
環山者三。——《戰國策·齊策》
九首蛇身自環。——《山海經·大荒北經》
4.又如：環回（循環，周轉）；環拜（盤鏇與直拜）；環激（鏇轉攪動）；環濤（迴旋的波濤）。
常用詞組
1.環靶huánbǎ
[roundtarget]由若干靶環套成靶面的靶子。
2.環保huánbǎo
[environmentalprotection]對環境進行保護。
環保辦公室。
砍掉那片樹不利於環保。
3.環抱huánbào
[encircle；surround；hemin]環繞，圍繞在中間。
古老的寺廟處於綠樹環抱之中。
4.環堵蕭然huándǔ-xiāorán
[inacold,bareroom]環堵：四面土牆。蕭然；蕭條的樣子。形容家中空無所有，極其貧困。
環堵蕭然，不蔽風日。——《陶淵明集·五柳先生傳》
5.環復huánfù
[encircle；surround]環繞
摺疊環復。——明·魏禧《大鐵椎傳》
6.環顧huángù
[driftaround；lookaround]四顧，觀察四周。
環顧其中。——唐·柳宗元《柳河東集》
環顧國內，賊氛方熾。——孫文《黃花岡七十二烈士事略序》
讓我的雙眼環顧房間。
7.環規huánguī
[ringgage]一種外徑規，其形式是圓筒形環或墊圈，常帶有淬硬鋼襯套。
8.環礁huánjiāo
[atoll]環狀的礁石
9.環節huánjié
（1）[link；sector]∶相互關聯的許多事物中的一個。
生產環節
（2）[annualring]∶在某些魚的鱗上的斑紋或隆起的脊，相當於一年的生長。
10.環境huánjìng
（1）[environment；surroundings；circumstance；ambience]
（2）周圍的地方
環境優美
（3）周圍的情況、影響或勢力。
換換環境
11.環境保護huánjìngbǎohù
[environmentalprotection]為了防止惡劣的氣候或其他廢水、廢氣、廢渣等環境因素危害而對人或設備所作的保護。
12.環鋸huánjù
（1）[trephine]
（2）作環形鋸開的一種外科手術器械。
（3）用這種器械施行手術。
13.環列huánliè
[lineupinacircle]環圍排列
將軍朝環列的侍衛看了幾眼，走了。
14.環裂huánliè
[ringshake；cupshake]一種介於同心層之間的木材裂縫。
15.環路huánlù
（1）[ringroad]∶環繞城市的道路。
增設環路
（2）[loop]∶閉合電路；閉合迴路。
16.環論huánlùn
[ringtheory]代數學中研究環的結構的分支。
17.環佩huánpèi
[jadependant（wornonagirdle）]環形玉佩；婦女的飾物。
小姐氣得把環佩都摔了。
18.環球huánqiú
（1）[roundtheworld]∶圍繞地球。
環球旅行
（2）[theearth；thewholeworld]∶全球，全世界。
19.環繞huánrào
（1）[encircle]∶沿由路程、行進和旅行所形成的圓圈運動。
環繞世界一周
（2）[surround]∶在四周構成圓環；構成彎曲或圓形邊界。
林地環繞著村莊
20.環山huánshān
（1）[aroundmountains]∶環繞著山
環山公路
（2）[surroundedbymountains]∶被山圍著
村子三面環山，村北是一片平地
21.環生huánshēng
[takeplaceoneafteranother]連續地發生。
環生支節
22.環蛇huánshé
[krait]環蛇屬（Bungarus）的幾種生有鮮明圈環，雖不愛尋釁但卻極毒的夜行性眼鏡蛇型蛇的任一種，土生於東亞及其附近島嶼上，常出現於耕地和居民點附近，特別愛吃其他種蛇。著名的兩種環蛇是金環蛇（B.fasciatus）和銀環蛇（B.multicinctus），中國南方各省都有。
23.環視huánshì
[lookaround]向四面觀看；環顧。
老師走進教室，環視一周之後才開講。
24.環水huánshuǐ
[waterlocked]幾乎被水包圍的
環水的陸岬
25.環鎖huánsuǒ
[ringlock]一種字碼鎖，套在鎖簧周圍的一串帶槽環必須這樣安排，使得在鎖簧閂上以前各槽與鎖簧卡住。
26.環眺huántiào
[lookaroundintothedistance]環視眺望
登上長城環眺，萬物盡收眼底
27.環衛huán-wèi
[environmentalsanitation]環境衛生的簡稱。
在環衛戰線上乾一輩子
28.環形huánxíng
（1）[ringy]∶圓環形狀的
（2）[annular]∶形狀像環
植物的環形子房室
29.環鏇huánxuán
[curlup；windaround]迴環繚繞
香氣環鏇。——唐·李朝威《柳毅傳》
30.環遊huányóu
[travelaround]周行遊歷
環遊地球一周
31.環宇huányǔ
[thewholeworld]全世界
轟動環宇
32.環子huánzi
[ring]環圓形狀的物品。
套住環子往外拉
33.環鑽huánzuàn
（1）[trephine]
（2）作環形切除的一種外科器械。
（3）用這種器械施行手術。
環
正文
一個具有兩種二元運算的代數系統。設在集合 R中已定義了加法與乘法，而R在加法下是一個交換群,且乘法對加法有分配律，則R稱為一個非結合環。此時R中就有惟一的零元素θ，使得對α∈R恆有α+θ=α；R 中每個α有惟一的負元素-α,使α+(- α)=θ,可簡記α+(-b)為α-b。分配律可推廣為：α(b±с)=αb±αс，(b±с)α=bα±сα；用數學歸納法可證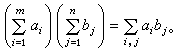
【(αα)b】 α=(αα)(bα)，那么R 稱為一個若爾當環。在非結合環的研究中,李環與若爾當環是內容最豐富的兩個分支。如果非結合環R 的乘法適合結合律，那么R 稱為一個結合環或環。如果在環R中再規定如下的一個新乘法“。”（稱為換位運算）：α。b=αb-bα，那么R 對原來的加法與新有的乘法是一個李環；若規定的新乘法為“·”（稱為對稱運算）:α·b=αb+bα，則R 便成一個若爾當環。
設S 是非結合環R 的一個非空子集，若對於R 的加法與乘法，S 也構成一個非結合環，則S 稱為R 的一個子環。一個真正的非結合環（即其中有三個元素在相乘時不適合結合律）的一個子環，有可能是一個結合環。非結合環R 的若干個子環的交，仍是R 的一個子環。當T 為R 的一個非空子集時，R 中所有含T 的子環的交顯然是R 中含T 的最小子環,稱之為R的由T 生成的子環。如果非結合環R 中任意三個元素生成的子環恆為結合環,那么R已經是一個結合環；如果R中任意兩個元素生成的子環恆為結合環,那么R稱為一個交錯環;如果R中任意一個元素生成的子環恆為結合環,那么R稱為一個冪結合環。在冪結合環中，第一、第二指數定律即
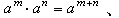
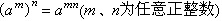恆成立。如果一個交錯環的乘法還適合交換律，那么它稱為一個交錯交換環。在交錯交換環中，不僅有第一、第二指數定律成立，而且有第三指數定律即
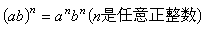成立；還有二項式定理。 結合環與交換環的典型例子如:F上的n階全陣環,即數域（或域）F上的所有n階矩陣在矩陣的加法與乘法下構成的一個環。V的完全線性變換環，即F上的一個向量空間 V的全部線性變換在變換的加法與乘法下構成的一個環。F上的多項式環，即F上一個或若干個文字的多項式全體構成的一個交換環。整數環，即全體整數構成的一個交換環；全體偶數構成它的一個子環，稱為偶數環。R上的n階全陣環,即在任意一個環R上的全部n階矩陣,對於仿通常矩陣的運算定義的加法與乘法構成的環，記為Rn。【0,1】上的全實函式環，即定義在區間【0,1】上的全部實函式，對於函式的加法與乘法構成的一個交換環。整數模n的環R奱，即模n剩餘類，對於剩餘類的加法和乘法構成的一個交換環。它是只含有限個元素的交換環的典型例子。
若一個環R中含有一個非零元素e≠θ，使對每個x∈R 有ex=xe=x,則e稱為R 的一個單位元素。一個環若有單位元素,則它必然是惟一的。設R是一個含有單位元素的環,α是R 中一個元素,若R 中有元素b,使αb=bα=e,則b稱為α的一個逆元素。當α有逆元素時,其逆元素必然是惟一的,記為α-1 ,α-1 也有逆元素,而且就是α,即(α-1 )-1 =α。R 的零元素θ 必無逆元素。若R 的每個非零元素都有逆元素, 則R 稱為一個體或可除環。四元數代數就是典型的體。在體的定義中再規定其乘法適合交換律，就是域的定義。
理想 設S是環R 的一個非空子集，所謂S是R 的一個左理想，意即①S 是R 作為加法群時的一個子群；②當α∈S,x∈R 時,則xα∈S。若有αx∈S,則S稱為R 的右理想。如果S 既是R 的左理想，又是R 的右理想,則稱S是R 的一個理想。例如,{θ}是環R 的一個理想。設l1、l2都是環R 的左理想。R中所有的元素α+b(α∈l1,b∈l2)作成R 的一個左理想,並稱之為l1與l2的和,記為l1+l2。R中所有的有限和
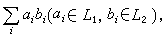作成R 的一個左理想,稱為R 的左理想l1與l2的積,記為l1l2。易知R的左理想的加法適合交換律與結合律；R 的左理想的乘法適合結合律且對加法有分配律。 對於R 的右理想的加法與乘法也有類似結果。由於左理想與右理想的對稱性,因此以下關於左理想的討論, 對於右理想也適合。環R 的兩個左理想的和的概念可以推廣成若干(有限或無限)個左理想li的和
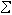li，它是由所有的有限和 
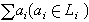所構成的。 如果這些li均非零, 而且在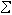li中每個元素α=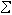αi的表法是惟一的，那么R的這組左理想li(i∈i)稱為無關的。環R 的兩個左理想的積的概念可以推廣成任意有限多個左理想l1，L2,…，ln的積l1l2…ln。特別，當這些li都是R 的同一個左理想 L時，此積簡記為ln 。設T是環R 的一個非空子集。R 中有元素α ,它能從左邊去零化T 中每個元素即αT=｛αt|t∈T｝是｛θ｝,例如R 中的零元素θ 就是這樣一個元素。R 中所有這種元素作成R 的一個左理想, 稱為T 在R 中的左零化子，或R 中的一個左零化子。 如果環R 的任意一組左理想中恆存在極小的左理想，那么環R 稱為滿足左極小條件, 或降鏈條件。所謂極小左理想,是指一組左理想中的一個左理想,它不能真正的包含組中任何左理想。同理可定義環R的左極大條件(或升鏈條件) 以及環R 的左零化子的極小與極大條件。由於環R 的左零化子僅僅是R 的一類特殊的左理想，所以環R 的左零化子的極小與極大條件,分別弱於R的左極小與左極大條件。若環R 滿足左極大條件，則R 中左理想的任何無關組必為有限的。滿足左極小條件的環又稱為左阿廷環；滿足左極大條件的環又稱為左諾特環；一個環滿足條件：①它的左理想的任何無關組恆為有限的；②它的左零化子滿足極大條件，稱為左哥爾迪環。由上述可知，左諾特環恆為左哥爾迪環。
設N是環R 的一個理想。首先,R 作為一個(交換)加法群時，則N 就是群R 的一個正規子群。N 在R 中的全部陪集對於陪集的加法(α+N)+(b+N)=(α+b)+N 作成一個(交換)加法群。其次,規定(α+N)(b+N)=αb+N,這與陪集的代表元素α、b的取法無關。易知陪集的這種乘法，適合結合律且對加法有分配律。於是就得到一個環，並稱之為環R 關於其理想N 的剩餘類環，記為R/N。它與環R有同態關係。所謂同態，是指對於兩個環R1、R2,有一個從R1 到R2上的映射σ：R1→R2，使對任意 α·b∈R1恆有σ(α+b)=σ(α)+σ(b),σ(αb)=σ(α)σ(b)。R2是R1在σ下的同態像,記為
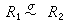。對任意環R 及其任意理想N ,只要定義σ(α)=α+N 就得到R 到R/N上的一個同態映射,特稱之為自然同態映射。如果環R1到環 R2上的一個同態映射σ，又是一一映射,那么σ 稱為同構映射,記為
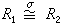。可以證明, 如果σ 是環R 到環R′上的一個同態映射，那么R中所有滿足 σ(α)=θ′∈R′的元素構成R的一個理想N，稱為σ的核，且有R/N≌R′；如果環R滿足左極小（或極大）條件，那么其任意同態像亦然。 設l是環R 的一個左理想，如果有正整數n使ln ={θ}，那么l稱為冪零的。如果對l中每個元素α恆有正整數n(α)使
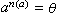,那么l稱為詣零的。顯然冪零左理想必為詣零左理想,但反之則未必。對R的右理想也有相應的定義。如果P是環R 的一個理想,而對R 的任意兩個理想A、B，只要AB嶅P，就必有A嶅P 或B嶅P,則P 稱為R 的一個質理想或素理想。如果環R 的零理想｛θ｝是R 的一個質理想，那么R 稱為一個質 (素)環。如果環R 除｛θ｝外不再含其他的冪零理想，那么R 稱為一個半質(素)環。質環恆為半質環，但反之則未必。 結構理論 設R1,R2,…,Rm均為環R的非零子環。如果R的每個元素α均可惟一地表為
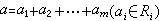，且當i≠j時恆有
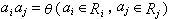,那么R 稱為R1，R2,…,Rm的環直接和(或簡稱直和),記為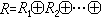
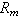。此時諸 Ri均必為環R 的理想且R 滿足左極小（極大）條件，必要而且只要諸Ri均然。當一個非零的環不能表為兩個以上的非零子環的環直接和時，則稱之為不可分環。例如非零的單純環(即除｛θ｝與自身外不再含其他理想的環)就是不可分環。 一個非零的環R 為左阿廷質環,必要而且只要有體K使
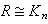。此時若又有體T使
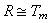,則必有T≌K,m=n。這樣的環必為單純環，又稱為阿廷單純環。一個非零的環為左阿廷半質環，必要而且只要它是有限個阿廷單純環的環直接和。這樣的環又稱為阿廷半單純環。一個阿廷半單純環為不可分環，必要而且只要它是阿廷單純環。以上結果統稱為韋德伯恩-阿廷結構定理。設R 是任意一個左阿廷環,於是R 的詣零左、右理想恆為冪零的;R 的所有冪零左理想的和又等於R 的所有冪零右理想的和, 從而這個和N 是R 的惟一最大冪零理想,稱為R 的根,而且當N <R 時，剩餘類環R/N 是阿廷半單純環。 對環R 中元素α，如果存在 α′∈R，使α+ α′+αα′=α+α′+α′α=θ,那么α稱為擬正則的 ,而且α與α′互為擬逆。例如,詣零元素α就是擬正則的，當αn =θ時，α′=-α+α2 -
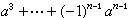。又如整數環中的－2 也是擬正則的,其擬逆即－2自己。如果環R 的一個左(或右)理想l的每個元素α都是擬正則的(此時α的擬逆α′亦必在l中),那么l稱為R 的一個擬正則左(或右)理想。任意環R中恆存在惟一的最大擬正則理想J,稱為R的雅各布森根,它包含R 的所有擬正則左與右理想,且剩餘類環R/J不含非零的擬正則左與右理想。特別,當J=｛θ｝時, R 稱為雅各布森半單純環。於是任意環R 關於其雅各布森根J 的剩餘類環R/J,便恆為雅各布森半單純環。非零的滿足左極小條件的雅各布森半單純環就是阿廷半單純環。 左分式環 如果在環R 中有α≠θ,b≠θ,而αb=θ,那么α稱為左零因子，b稱為右零因子。一個非零元素如果既非左零因子，又非右零因子，那么這個非零元素稱為正則元。設Q是一個有單位元素e的環,R是它的一個子環，如果R的每個正則元α在Q中有逆元素α-1 ,且Q中每個元素β均可表為β=α-1 b(其中α、b∈R且α為正則元)，那么Q稱為R 的一個左分式環。設R 是一個非零的環，則R 是哥爾迪質環, 必要而且只要R 有一個左分式環為阿廷單純環；R 是哥爾迪半質環,必要而且只要R有一個左分式環為阿廷半單純環。
所謂環R 是一個左奧爾環，即指R 含有正則元而且滿足左奧爾條件：對α、b∈R（其中b為正則元），恆有α1、b1∈R(其中 b1是正則元)使得b1α= α1b。當環R無零因子時，左奧爾條件即R 中任二非零元有共同的非零左倍元。一個環R有左分式環，必要而且只要R是一個左奧爾環。
序環 所謂環R的偏序關係“≤”,是指“≤”在環R的元素之間具有以下性質：①自反性,即對每個α∈R恆有α≤α；②傳遞性,即當α≤b，b≤с時有α≤с；③反對稱性，即當α≤b，b≤α時有α=b；④如果α≤b，那么對x∈R恆有α+x ≤b+x；⑤當θ≤α,θ≤b時有θ≤αb。有偏序關係存在的環，稱為偏序環。在偏序環中，當α≤b,с≤d時,就必有α+с≤b+d;當α≤θ，θ≤b時,就有αb≤θ，bα≤θ；當α≤θ，b≤θ 時,就有θ≤αb。在偏序環中,若α≤b且α≠b，則記為α<b。當θ<α時則稱α是一個正元素；當b<θ時則稱b是一個負元素。當α為正元素時，則－α必為負元素；當b為負元素時，則－b必為正元素；當偏序環中無左、右零因子時，就有兩個同號元素（即同為正元素或同為負元素）相乘為正；兩個異號元素相乘為負。如果偏序環R 中任意兩個元素α、b均有α≤b或者b≤α，那么就說R 是一個序環。例如整數環在通常數的小於等於關係“≤”下就是一個序環。
發展概況 環論的發展可追溯到19世紀關於實數域的擴張及其分類的研究。F.G.弗羅貝尼烏斯、J.W.R.戴德金、É.(-J.)嘉當、W.R.哈密頓和T.莫利恩等人是發展超復系理論的主要數學家。後來，發展成一般域上的代數結構理論，是源於J.H.M.韋德伯恩在1907年發表的著名論文。A.A.阿爾貝特、R.（D.）布饒爾及（A.）E.諾特等人發展與簡化了單純代數理論與算術的理想理論，在1927年E.阿廷的論文又把代數結構的主要結果推廣到具極小條件的環上,而成為韋德伯恩-阿廷結構定理。此後對於不具鏈條件的環換成一些拓撲或度量的條件進行研究，如J.馮·諾伊曼與F.J.默里在希爾伯特空間中研究變換環,馮·諾伊曼的正則環理論與И.М.蓋爾范德的賦范環論等。19世紀40年代後，一般環的根理想理論應時而起，迅速發展，其中尤以雅各布森根與半單純環以至本原環理論較為系統而深入。1958年A.W.哥爾迪對具極大條件的環得到了至善的結果。在體論以及非結合環中的若爾當環與雅各布森環的研究，近年來均甚為活躍。
參考書目
N. Jacobson,Structure of Rings,2nd ed., Amer. Math.Soc., Providence, R.I.,1964.
N.J.Divinsky,Rings and radicals,George Allen & Unwin, London,1965.
F.A.Száiz,radicals of Rings,Akadémiai Kiad圝, Budapest,New York, 1981.
配圖
數學分支
近世代數的一個概念
近世代數參見張禾瑞主編的《近世代數基礎》
