Mallows's Cp

在統計學中，馬洛斯(Colin Lingwood Mallows)提出運用C去評估一個以普通最小二乘法(Ordinary Least Square或OLS)為假設的線性回歸模型的優良性，從而用於模型選取(Model Selection)。當模型中含有多個自變數(Independent Variables或Explanatory Variables)，使用Mallows’s C 可以為模型精選出自變數子集。C數值越小模型準確性越高。對於高斯線性模型(Gaussian Linear Regression)，馬洛斯的Cp值被證明與赤池信息準則(Akaike Information Criterion或AIC)等效。 其他模型選取方法還有貝葉斯信息準則(Bayesian Information Criterion 或BIC)以及調整後的R方(Adjusted R-Squared)。

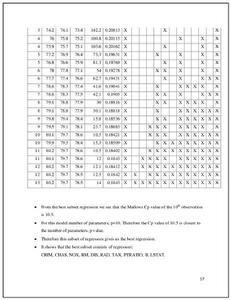
原理

模型選擇統計量如殘差平方和(Residual Sum of Squares)隨著模型包含的自變數數量增多而減少，由此可導致過度擬合(Overfitting)的問題，即自變數數量過多導致模型預測能力下降。藉助Mallows’s C p 篩選自變數子集可以有效控制參數數量，從而達到最佳化模型的目的。 C p統計量的計算基於一個數據樣本，用於估計均方預測誤差(Mean Squared Prediction Error 或MSPE)作為總體目標值:

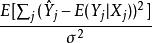Mallows's Cp

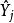Mallows's Cp

指代在j情形下回歸模型中的擬合值(fitted Value)

指代在j情形下回歸模型中的期望值(Expected Value)

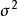Mallows's Cp

指代誤差方差，假設在各情形下保持不變

MSPE不一定隨著自變數數量的增加而減少。最優模型條件由樣本大小(Sample Size)，自變數數量及組合以及其間的多元共線性(Collinearity)共同決定。

假設及定義

假設

假設線性 原回歸模型(Full Model)：

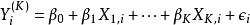Mallows's Cp

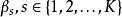Mallows's Cp

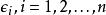Mallows's Cp

模型自變數係數為 ; 模型誤差為

如果K>p, 從K個自變數中篩選p個回歸自變數， 子回歸模型(Reduced Model)：

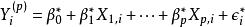Mallows's Cp

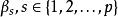Mallows's Cp

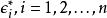Mallows's Cp

模型自變數係數為 ;模型誤差為

定義

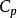Mallows's Cp

以 原回歸模型為基礎，其可能的一個 子回歸模型的 統計值 定義為

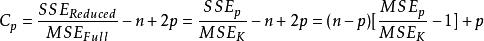Mallows's Cp

，

其中, n是樣本大小，MSE是均方誤差（Mean Square Error），SSE是誤差平方和(Sum of Square Error)

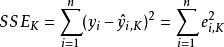Mallows's Cp

，指代 原回歸模型中的誤差平方和

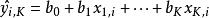Mallows's Cp

，指代在含K個自變數的線性回歸模型中對第i個y樣本數據的擬合值

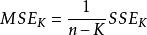Mallows's Cp

，指代 原回歸模型中的均方誤差

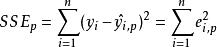Mallows's Cp

，指代 子回歸模型中的誤差平方和

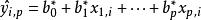Mallows's Cp

，指代在含p個自變數的線性回歸模型中對第i個y樣本數據的擬合值

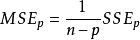Mallows's Cp

，指代 子回歸模型中的均方誤差

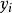Mallows's Cp

指代y因變數的第i個樣本數據的真實值；

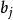Mallows's Cp

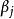Mallows's Cp

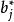Mallows's Cp

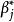Mallows's Cp

根據線性回歸模型的假設，其中包括對普通最小二乘法以及對模型誤差分布的假設，是的估計值； 是 的估計值。

局限性

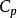Mallows's Cp

1. 需要大的樣本以提高 準確性

2. 在特徵選擇(Feature Selection)中不能處理複雜模型組合情況

實用性

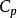Mallows's Cp

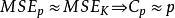Mallows's Cp

通常，當 接近或小於p時，可停止篩選並採用該自變數子集為最佳組合，即 ，也就是採用數量較少的自變數組合來簡化模型的同時，也能保持模型的均方誤差不變或減小。同時緩解了過度擬合問題以及提升了模型的預測能力。