L2空間

簡介

L 空間是平方可積函式類，它更接近於n維歐氏空間，具有n維歐氏空間許多類似的幾何性質。

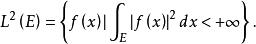L2空間

若E是R 內的可測集，而f(x)在E上可測且|f(x)| 在E上勒貝格可積，則稱f(x)在E上是平方可積的。所有這樣的函式之集稱為E上的L 空間，記為L (E)或L ，即

性質

L 空間的主要性質有：

1、L (E)是線性空間，其中零元素是E上幾乎處處為零的函式。

2、（施瓦茲不等式）若f(x),g(x)∈L (E)，則f(x)g(x)∈L(E)，且有

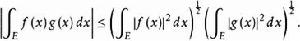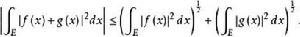L2空間

L2空間

3、（柯西不等式）若f(x),g(x)∈L (E)，則

範數性質

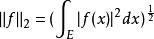L2空間

對於f(x)∈L (E)，令 ，||f||具有以下性質：

1、（非負性）||f||≥0，且||f||=0若且唯若f(x)=0幾乎處處收斂於E。

2、（正齊性）對任意實數α，有||αf||=|α|||f||。

3、（三角不等式）||f+g||≤||f||+||g||。

因此，||f||是L (E)上的一個範數。進一步，L (E)是希爾伯特空間。