定義
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲定義1 給定集合X的一個點以及空間的一個開集,令
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲所有集合構成的拓撲的一個子基,這個拓撲稱為 點態收斂拓撲(topology of pointwise convergence)或 點開拓撲(point-open topology)。
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲這個拓撲的一般基元素是子基元素的有限交,因此,包含函式的一個典型的基元素就是由所有在有限多點處“接近”的函式組成,這樣的鄰域如圖1所示,它由所有函式圖像與所給三個垂直區間都相交的函式構成。
 圖1
圖1 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲上的點態收斂拓撲就是 積拓撲,如果我們用J代替X,將J的一般元素記為,這樣看起來就更加熟悉了,這時,使得的所有函式構成的集合恰好就是的子集而它也正好就是積拓撲的標準子基元素。
相關知識
稱其為點態收斂拓撲的理由緣於以下定理:
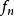 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲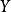 點態收斂拓撲
點態收斂拓撲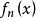 點態收斂拓撲
點態收斂拓撲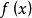 點態收斂拓撲
點態收斂拓撲定理1 在點態收斂拓撲下,函式序列收斂於函式, 若且唯若對於每一個點中點的序列收斂於點。
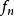 點態收斂拓撲
點態收斂拓撲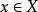 點態收斂拓撲
點態收斂拓撲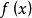 點態收斂拓撲
點態收斂拓撲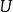 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲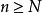 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲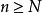 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲證明: 這是積拓撲中一個一般性的事實,在這裡我們使用函式記號來證明它,假定在點態收斂拓撲之下收斂,給定及含有的開集,集合是的一個鄰域,因此存在整數N,使得對於所有的,有於是對於所有的,。
 點態收斂拓撲
點態收斂拓撲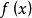 點態收斂拓撲
點態收斂拓撲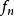 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲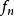 點態收斂拓撲
點態收斂拓撲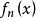 點態收斂拓撲
點態收斂拓撲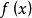 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲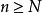 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲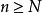 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲反之,設對每個收斂子,要證明在點態收斂拓撲之下收斂於,只要證明如果是包含的任意一個子基元素,則對於充分大的n,包含所有的就足夠了(為什麼?)。但是因為收斂於,並且,所以必存在一個整數N,使得對於有,於是對於,。
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲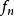 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲例1 考慮空間R ,其中定義為的連續函式序列()在點態收斂拓撲下收斂於函式,其中的定義為
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲這個例子說明,在點態收斂拓撲下,連續函式的子空間不是R 中的閉集。
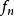 點態收斂拓撲
點態收斂拓撲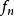 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲我們知道,若一個連續函式序列()在一致拓撲下收斂,則極限必定是連續的,然而上面這個例子說明,一個序列僅在點態收斂拓撲下收斂,卻未必有連續的極限,人們可能要問,是否存在某一個拓撲介於這兩個拓撲之間,仍能保證連續函式的收斂序列有連續的極限呢?答案是肯定的,只要對空間X加一點限制,而且這個限制還相當寬泛,即要求X是緊緻生成的,如果在以下定義的緊緻收斂拓撲下,()收斂於,就足以保證是連續的了。
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲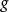 點態收斂拓撲
點態收斂拓撲定義2 設是一個度量空間,X是一個拓撲空間,給定的一個元素,X的一個緊緻子空間C以及一個數令表示中所有滿足下式的元素構成的集合:
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲這些集合組成了的一個拓撲基,我們稱這個拓撲為 緊緻收斂拓撲(topology ofcompact convergence)(有時也稱它為“緊緻集合上的一致收斂拓撲”)。
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲易見這些集合滿足作為基的條件,最關鍵的一步是注意,若,則對
 點態收斂拓撲
點態收斂拓撲 點態收斂拓撲
點態收斂拓撲有。

