魏爾斯特拉斯判別法

魏爾斯特拉斯判別法（Weierstrass Discriminance）是分析學中一條十分重要的判定法則，主要用於判定數項級數的收斂、函式項級數的一致收斂、反常積分的收斂以及反常含參積分的一致收斂等。

原理

魏爾斯特拉斯判別法是一個類似於比較審斂法的判別法 ，可以用於判斷函式項級數的收斂性。

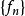魏爾斯特拉斯判別法

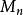魏爾斯特拉斯判別法

假設 是定義在集合A內的一個實數或複數函式的數列，並存在正的常數 ，使得

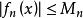魏爾斯特拉斯判別法

對於所有的n≥1和A內所有的x成立。進一步假設級數

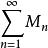魏爾斯特拉斯判別法

收斂。那么級數

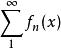魏爾斯特拉斯判別法

在A內一致收斂。

特性

如果函式的陪域是任何一個巴拿赫空間，則 魏爾斯特拉斯判別法的一個更一般的形式仍然成立，但要把

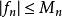魏爾斯特拉斯判別法

換成

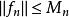魏爾斯特拉斯判別法

魏爾斯特拉斯判別法

其中 是巴拿赫空間的範數。