集合的覆蓋與劃分
劃分
 集合覆蓋
集合覆蓋 集合覆蓋
集合覆蓋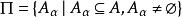 集合覆蓋
集合覆蓋設A是非空集,稱 是集合A的 劃分,若 是A的非空子集的集合,即 ,且滿足 :
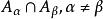 集合覆蓋
集合覆蓋① ;
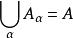 集合覆蓋
集合覆蓋② 。
覆蓋
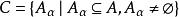 集合覆蓋
集合覆蓋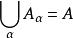 集合覆蓋
集合覆蓋非空集A的一個 覆蓋C是A的非空子集的集合,即 ,滿足 。
集合的覆蓋與劃分的區別在於:覆蓋不要求各個子集兩兩之交為空集。
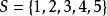 集合覆蓋
集合覆蓋例1 設集合 ,則
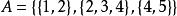 集合覆蓋
集合覆蓋(1) 是S的一個覆蓋,不是劃分,因為不滿足劃分定義中的條件①:
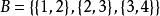 集合覆蓋
集合覆蓋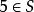 集合覆蓋
集合覆蓋(2) 不是S的覆蓋,更不是劃分,因為B的任意一個子集均沒有元素 ;
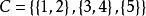 集合覆蓋
集合覆蓋(3) 是S的覆蓋,也是其劃分。
任一給定集合S,其覆蓋或劃分,均不一定是唯一的:給定了非空集合S的一個覆蓋或劃分,則S唯一確定 。
最佳化求解問題
基本介紹
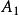 集合覆蓋
集合覆蓋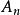 集合覆蓋
集合覆蓋集合覆蓋是一種最佳化求解問題,對很多組合數學和資源選擇問題給出了漂亮的抽象模型。問題是這樣的:給定一個集合s,集合P由集合S的子集到組成,集合C由集合P中的一個或多個子集組成。如果S中的每個成員都包含在C的至少一個子集中則稱集合C覆蓋集合S。此外,C包含的P的子集應該越少越好 。
舉例
圖1中的點代表一組城鎮。在國家建設規劃的初期,需要決定在什麼地方建設一些新的學校。這裡有兩個具體的要求:一是所有的學校都必須建在城鎮上,二是從任意一個城鎮出發,都應該可以在30英里的範圍到到達其中的某一所學校。那么,最少需要建多少所學校呢?
 圖1(a) 11個城鎮
圖1(a) 11個城鎮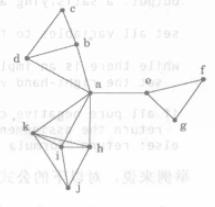 圖1(b) 相互距離在30英里內的城鎮
圖1(b) 相互距離在30英里內的城鎮 集合覆蓋
集合覆蓋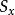 集合覆蓋
集合覆蓋 集合覆蓋
集合覆蓋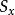 集合覆蓋
集合覆蓋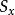 集合覆蓋
集合覆蓋這是一個典型的集合覆蓋問題。對每個城鎮,令為在其30英里範圍內的城鎮集合。建在的學校顯然能夠“覆蓋”中的所有城鎮。於是我們的問題就是,需要多少個這樣的才能覆蓋全國的所有城鎮 。
集合覆蓋問題
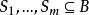 集合覆蓋
集合覆蓋輸入:元素集合B。集合。
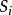 集合覆蓋
集合覆蓋輸出:選出的一部分集合,使其並為B。
成本:所選出的集合數量。
(在我們的例子中,集合B中的元素就是城鎮。)這個問題本身很自然地引出了如下的 貪心解法 。
不斷重複:直到B中的所有元素都被覆蓋:
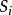 集合覆蓋
集合覆蓋選取包含未被覆蓋元素的最大集合。
 集合覆蓋
集合覆蓋這是極其自然和符合直覺的。讓我們看看它如何處理此前的那個小例子。首先它會在城鎮建立一所學校,因為這樣能覆蓋最多的城鎮。此後,它將進一步選擇c,j以及f和g之一建立另三所學校。這樣最終所需的學校總數為4。不幸的是,實際上還存在一個更好的解,那就是將學校分別建在b、e和i,如此只需要三所學校就可以覆蓋所有城鎮。在這裡貪心方法並不是最優的!
幸運的是,貪心算法的解與最優解的距離其實並不遙遠。
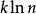 集合覆蓋
集合覆蓋斷言 設B有n個元素,且其最優覆蓋共包含k個集合,則貪心算法所得結果最多包含個集合。
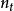 集合覆蓋
集合覆蓋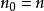 集合覆蓋
集合覆蓋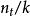 集合覆蓋
集合覆蓋設為貪心算法中經過t次疊代後仍未覆蓋的元素數量(顯然)。由於這些剩餘的元素能被最優的k個集合覆蓋,因此,當前一定存在某個包含其中個元素的集合。這意味著,貪心策略能夠使得
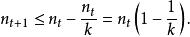 集合覆蓋
集合覆蓋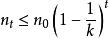 集合覆蓋
集合覆蓋從而。進一步,由
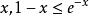 集合覆蓋
集合覆蓋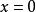 集合覆蓋
集合覆蓋“對任意,若且唯若時等號成立”
(以上不等式的正確性如圖2可證)
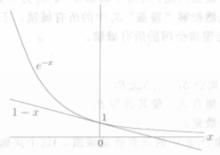 圖2 不等式的正確性
圖2 不等式的正確性可得
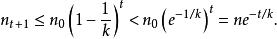 集合覆蓋
集合覆蓋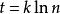 集合覆蓋
集合覆蓋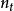 集合覆蓋
集合覆蓋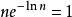 集合覆蓋
集合覆蓋因此當時,嚴格小於,即再也沒有未被覆蓋的元素了。
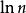 集合覆蓋
集合覆蓋 集合覆蓋
集合覆蓋貪心算法的解與實際的最優解的規模之比可能因問題輸入的不同而不同,但是總小於。對於某些特定的輸入,這一比例會非常接近於。我們稱這一最大比值為該 貪心算法的逼近因子。看起來對這樣的結果應該還有很大的改進餘地,但事實上這種改進的空間並不存在。目前已知的結論是,在某些廣泛成立的複雜性假設之下,可以證明對以上問題不存在具有更小逼近因子的多項式時間算法 。

