函式關係
部分子分布函式 部分子在水平上研究高能作用的最基本的物理量。利用部分子分布函式可以計算出雙噴柱關聯，單舉散射截面及帶電粒子多重分布，其函式關係式如下：
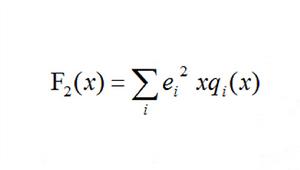部分子分布函式關係式
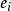部分子分布函式
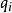部分子分布函式其中i是指核子中夸克種類數， 是第i種夸克所帶的電量，x是夸克所帶有的動量占核子動量的比例， (x)是第i種夸克的分布函式。部分子分布函式可分為積分的與未積分的部分分布函式，這裡的分布函式是積分的分布函式。
分類
積分部分子分布函式
積分部分子分布函式可用來描述深度非彈性散射實驗中的單舉反應、核子的內部結構等，它滿足傳統的扭度-2DGLAP方程。但是當部分子的密度很大時就必須考慮它們之間的相互作用，出現遮蔽效應，即高扭度現象。扭度-4DGLAP方程2修正後的演化方程。通過這兩個演化方程得到的積分部分子分布函式有著一定的差異性。當考慮Drell-Yan等高能過程時，橫動量過得作用則變得很重要，部分子不再依賴於一個標度，而要引入未積分部分子分布函式。
未積分部分子分布函式
未積分部分子分布函式沒有對橫動量進行積分的函式，它可由CCFM方程得到，但是CCFM方程只用於蒙特卡羅方法計算，非常複雜。
研究現狀
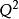部分子分布函式夸克的色禁閉性使得人們沒有辦法直接測出部分子的分布函式，必須通過擬合截面等試驗數據來確定積分部分子初始函式分布，然後根據演化方程得到大 下的積分分布函式，但是非微擾的標度沒有定論，不同的實驗小組如GRV、MARST等均提出了在不同的固定演化起點下的初始演化分布。標準動力學演化方程考慮了扭度-2效應，這時就需考慮扭度-4效應了。
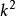部分子分布函式雖然對核子中的未積分部分子分布函式進行了理論和實驗方面的研究，但是對未積分部分子分布函式了解還是不夠多，究其原因主要在於：未積分部分子分布函式至少依賴兩個變數（x和 ）,微擾區域與非微擾區域的界限並沒有定論。一般採用的是GBW(Golec-Biernat-Wusthoff)模型，BFKL模型和KMR模型等。不同模型和初始分布下的未積分部分子分布函式都能解釋某些實驗現象，但是它們之間的共同性還不是很清楚。
