定義
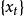 負指數衰減
負指數衰減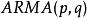 負指數衰減
負指數衰減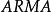 負指數衰減
負指數衰減若平穩時間序列 適合於模型,則其自相關函式,偏相關函式都是按 負指數衰減,這一特點是由 模型相應的線性差分方程的性質所決定,通常稱這種特性為拖尾性,因此實踐中可用來對模型進行識別。
性質
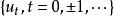 負指數衰減
負指數衰減設為實序列,滿足齊次線性差分方程
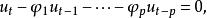 負指數衰減
負指數衰減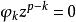 負指數衰減
負指數衰減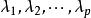 負指數衰減
負指數衰減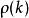 負指數衰減
負指數衰減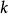 負指數衰減
負指數衰減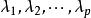 負指數衰減
負指數衰減差分方程相應的特徵方程為 ,設其根為 。其自相關函式當充分大時也滿足上述差分方程,故可表示為特徵根次冪的線性組合。
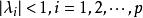 負指數衰減
負指數衰減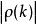 負指數衰減
負指數衰減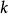 負指數衰減
負指數衰減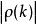 負指數衰減
負指數衰減若,則具有平穩解。若特徵根皆實根,則依 單調衰減;若存在單位圓內的復根,則呈共軛對出現,方程通解中含正弦餘弦項,呈 振盪式衰減,其典型圖形如下:
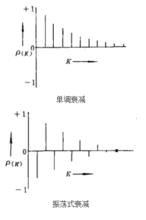 負指數衰減
負指數衰減套用-格林函式預報法
 負指數衰減
負指數衰減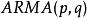 負指數衰減
負指數衰減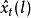 負指數衰減
負指數衰減 負指數衰減
負指數衰減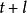 負指數衰減
負指數衰減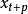 負指數衰減
負指數衰減格林函式預報法是平穩時間序列的一種直接預報方法。設觀察序列為模型,表示在時刻對未來時刻的值所作的平穩線性預報,則格林函式預報法由模型參數遞推計算格林函式
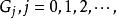 負指數衰減
負指數衰減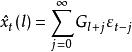 負指數衰減
負指數衰減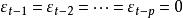 負指數衰減
負指數衰減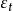 負指數衰減
負指數衰減然後,取值,可按
 負指數衰減
負指數衰減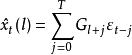 負指數衰減
負指數衰減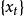 負指數衰減
負指數衰減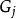 負指數衰減
負指數衰減 負指數衰減
負指數衰減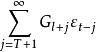 負指數衰減
負指數衰減遞推計算。該公式包含無窮項求和,實際上只可能用充分多項的有窮和近似,即。由的平穩性保證了是 負指數衰減的,當充分大時,小於給定精度。
