角動量算符對易關係

在量子力學中，角動量算符之間的對易關係是基本的對易關係之一。從這些對易關係出發就足以得出關於角動量算符及其本徵函式的許多性質，而不需要關心角動量算符在某個表象下的具體表達式。從數學上看，這一套理論實際上是研究與李代數su(2) 相關的性質。

基本信息

• 中文名：角動量算符對易關係
• 英文名：Angular momentum operator

簡介

在三維空間中的角動量算符（經典角動量的量子化）滿足下列的基本對易關係式：

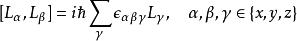角動量算符對易關係

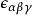角動量算符對易關係

式中 是列維-奇維塔符號。

上面的關係式反映了角動量算符的內在性質。反過來，可以直接由這組對易關係式出發，把滿足這樣性質的算符都稱為角動量算符。

定義

若有三個算符

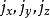角動量算符對易關係

滿足對易關係

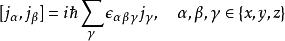角動量算符對易關係

則稱以這三個算符為分量的矢量算符

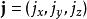角動量算符對易關係

為一個 角動量算符。

這樣定義的角動量算符自然地包含了軌道角動量、自旋角動量、總角動量等。

運用叉乘的符號，上面的 對易關係式 也可以簡單表示為：

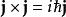角動量算符對易關係

角動量平方算符

定義角動量平方算符為

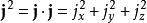角動量算符對易關係

直接計算可以得到：

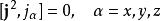角動量算符對易關係

升算符與降算符

進一步定義

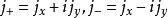角動量算符對易關係

它們分別稱為升算符與降算符，則直接計算可以得到下列關係式：

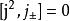角動量算符對易關係

1）

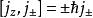角動量算符對易關係

2）

角動量算符對易關係

3）

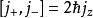角動量算符對易關係

4）

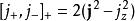角動量算符對易關係

5）

最後一式中的是 反對易子。