定義
設體系的能量本徵方程為
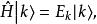 能量表象
能量表象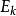 能量表象
能量表象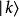 能量表象
能量表象方程中 為第k個能量本徵值,對應的本徵函式為 。這些本徵函式滿足正交歸一性
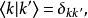 能量表象
能量表象和完備性
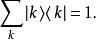 能量表象
能量表象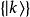 能量表象
能量表象於是, 可作為完備的基組,該基組所定義的表象為能量表象。
體系中的相關計算
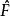 能量表象
能量表象在原子分子物理和材料物理的理論計算中,常常會在能量表象中求解體系的物理問題。例如,體系的一個力學量算符 ,其本徵方程為
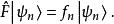 能量表象
能量表象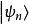 能量表象
能量表象有時,直接求解這個方程會很困難,在能量表象中求解會比較方便。對此,將本徵態 在能量表象中展開:
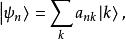 能量表象
能量表象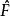 能量表象
能量表象代人 的本徵方程
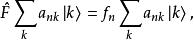 能量表象
能量表象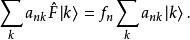 能量表象
能量表象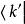 能量表象
能量表象用 左乘上式,得
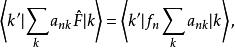 能量表象
能量表象即
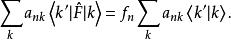 能量表象
能量表象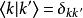 能量表象
能量表象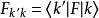 能量表象
能量表象利用關係式 ,並令 ,有
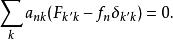 能量表象
能量表象上式為線性方程組。在矩陣理論中,上式可寫為矩陣方程,該方程有非平庸解的條件是
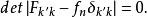 能量表象
能量表象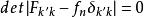 能量表象
能量表象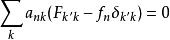 能量表象
能量表象 能量表象
能量表象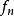 能量表象
能量表象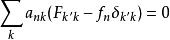 能量表象
能量表象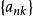 能量表象
能量表象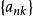 能量表象
能量表象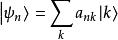 能量表象
能量表象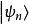 能量表象
能量表象由方程 可解出矩陣方程 中的本徵值 ,再將每個 值代入式 可解出相應的 。將 代人式 就可獲得I妒 。
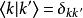 能量表象
能量表象必須指出的是,上述的數學過程中我們已經假定了基矢間是相互正交的。如前所述,基矢間的正交性不是必須的;在處理許多實際的物理體系(如分子、固體等)時,有時所選擇的基矢彼此之間並不正交,此時,式 不再保留,而代之為
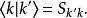 能量表象
能量表象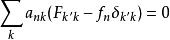 能量表象
能量表象相應地,方程 改為廣義矩陣本徵方
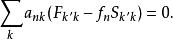 能量表象
能量表象通過對該方程的求解,可獲得體系的本徵值和本徵態。
