基本概念
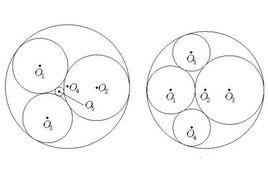
給出△ABC,以頂點A,B,C為圓心,作三個圓兩兩相切,並作與⊙A,⊙B,⊙C都外切的圓⊙S,以及與⊙A,⊙B,⊙C都相內切的圓⊙S'。
⊙S稱為 內索迪(Soddy)圓,⊙S'稱為 外索迪圓,如圖1 。
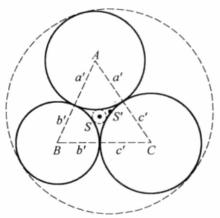 圖1
圖1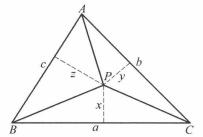 圖2
圖2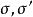 索蒂圓
索蒂圓英國的化學家索迪(Frederick Soddy,1877-1958)求出了這些圓的半徑 ,它們是
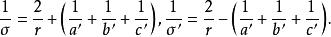 索蒂圓
索蒂圓事實上,這些結果在17世紀已經被笛卡爾發現 。
索迪線
內索迪圓圓心S和外索迪圓圓心S'的連線稱為 索迪線,由於內心和熱爾崗點也在此直線上,故也把聯結I和熱爾崗點Ge的直線稱為索迪線。它的三線方程是
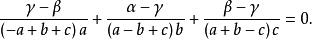 索蒂圓
索蒂圓索迪線上S',I,S和Ge成調和點列,索迪線垂直於熱爾崗線。
相關性質介紹
一個三角形ABC的歐拉線,上面有6個著名的點:垂心H,九點圓圓心N,重心G,外心O,德朗謝姆點Z,以及三角形的外接圓在A,B,C的切線所成三角形的外心。德朗謝姆點與H關於O對稱,是外接圓與斯坦納圓(以N為心,3R/2為半徑)的外相似中心(在斯坦納圓內,一個半徑為R/2的圓沿圓周滾動時,畫出有3個尖點的圓內旋輪線,它是西摩松線的包絡)。
採用通常的記號,以任一三角形ABC的頂點為圓心,s-a,s-b,s-c,或者s,s-c,s-b,或者s-c,s,s-a,或者s-b,s-a,s為半徑所作的3個圓兩兩相切。第一種情況如圖1所示,在其餘的每一種情況,一個圓包住另外兩個,對這3個圓的每一種情況,都可以找到另外兩個圓與它們都相切,稱這兩個圓為三角形的 索迪圓,並將它們的圓心與半徑記為
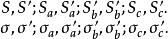 索蒂圓
索蒂圓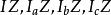 索蒂圓
索蒂圓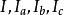 索蒂圓
索蒂圓其中σ< σ',等等,我們將發現這四對圓心落在4條直線上,其中是內心與旁心,而Z是德朗謝姆點 。
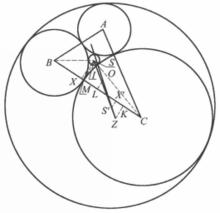 圖3
圖3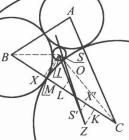 圖4 ( 圖3的放大圖)
圖4 ( 圖3的放大圖)在4R+r<2s時,第一對索迪圓的位置如圖1,令L為BC中點,X,X' ,M,K為S,S',I,Z在BC上的射影,容易得到關係
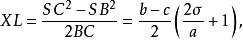 索蒂圓
索蒂圓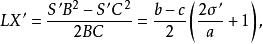 索蒂圓
索蒂圓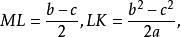 索蒂圓
索蒂圓因此
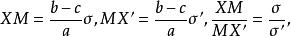 索蒂圓
索蒂圓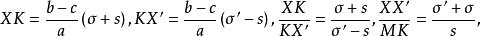 索蒂圓
索蒂圓因此I是索迪圓的內相似中心,S與S'在直線IZ上,Z分SS'為比(σ+s):(σ'-s),並且
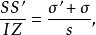 索蒂圓
索蒂圓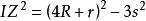 索蒂圓
索蒂圓容易算出,由此得出SS'的表達式,同時這也順便證明了
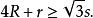 索蒂圓
索蒂圓(根據O.Bottema給H.S.M.Coxeter 的信,G.R.Veldkamp已經注意到外相似中心是約爾剛點,AM在這裡與自B,C引出的類似的塞瓦線相交)
在4R +r>2s時,類似的計算表明J是內相似中心,Z外分SS',比為(σ+s):(σ'+s),並且
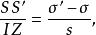 索蒂圓
索蒂圓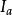 索蒂圓
索蒂圓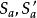 索蒂圓
索蒂圓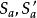 索蒂圓
索蒂圓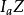 索蒂圓
索蒂圓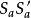 索蒂圓
索蒂圓對餘下的三對索迪圓,我們必須用旁心代替內心。例如,我們發現是圓心為的索迪圓的外相似中心。在直線上,Z內分比為(s-a-σ):(σ'-s+a)。
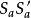 索蒂圓
索蒂圓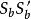 索蒂圓
索蒂圓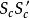 索蒂圓
索蒂圓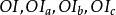 索蒂圓
索蒂圓圖5表明歐拉線HO與四條“索迪線"SS',,,都過Z點,為了避免圖形的複雜性,我們省掉了直線,雖然它們也是有些趣味的,因為它們是由內切圓與3個旁切圓在BC,CA,AB上的切點所成的4個三角形的歐拉線 。
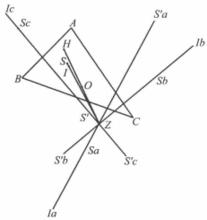 圖5
圖5