定理內容
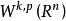索伯列夫嵌入定理 
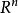索伯列夫嵌入定理 
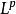索伯列夫嵌入定理 
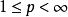索伯列夫嵌入定理 
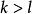索伯列夫嵌入定理 
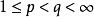索伯列夫嵌入定理 
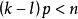索伯列夫嵌入定理 令 表示包含 上所有滿足前k階弱導數屬於 的實值函式的索伯列夫空間，其中k是非負整數且有1 。 索伯列夫嵌入定理的第一部分指出如果 且 滿足 和
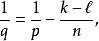索伯列夫嵌入定理 那么，
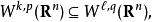索伯列夫嵌入定理 
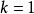索伯列夫嵌入定理 
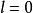索伯列夫嵌入定理 並且該嵌入連續。在 且 的特殊情形，Sobolev嵌入定理給出
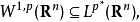索伯列夫嵌入定理 其中 p是p的Sobolev共軛，如下給出
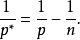索伯列夫嵌入定理 這個索伯列夫嵌入定理的特例可由 索伯列夫不等式直接得出。
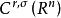索伯列夫嵌入定理 
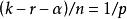索伯列夫嵌入定理 
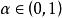索伯列夫嵌入定理 索伯列夫嵌入定理的第二部分用於嵌入到Hölder空間 。如果 其中 ，則有嵌入
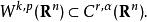索伯列夫嵌入定理 索伯列夫嵌入的這個部分可由Morrey不等式直接得出。直觀的說，這種包含關係表示足夠高階的弱導數存在性意味著一些經典導數的連續性 。
推廣
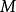索伯列夫嵌入定理 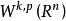索伯列夫嵌入定理 索伯列夫嵌入定理對於有其他適當定義域的索伯列夫空間也成立。特別的，索伯列夫嵌入的兩個部分在滿足下列條件時成立 ：
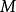索伯列夫嵌入定理 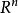索伯列夫嵌入定理 1)是上有Lipschitz邊界的有界開集（或者邊界滿足錐條件）；
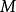索伯列夫嵌入定理 2)是緊黎曼流形；
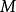索伯列夫嵌入定理 3)是有Lipschitz邊界的緊帶邊黎曼流形；
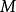索伯列夫嵌入定理 
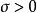索伯列夫嵌入定理 4)是滿足單射半徑且截面曲率有界的完備黎曼流形。
索伯列夫不等式
索伯列夫不等式，即Gagliardo–Nirenberg–Sobolev不等式，可以用於證明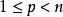索伯列夫嵌入定理。
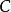索伯列夫嵌入定理 
索伯列夫嵌入定理 
索伯列夫嵌入定理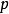 
索伯列夫嵌入定理 假設u是 R上擁有緊支集的連續可微實值函式。對於存在常數隻依賴於和使得
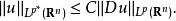索伯列夫嵌入定理 
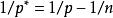索伯列夫嵌入定理 
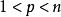索伯列夫嵌入定理 
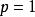索伯列夫嵌入定理 其中。的情形由Sobolev給出，的情形由Gagliardo和Nirenberg獨立給出。Gagliardo–Nirenberg–Sobolev不等式直接導出Sobolev嵌入
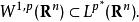索伯列夫嵌入定理 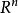索伯列夫嵌入定理 上其他階的嵌入可由適當的疊代得到。
