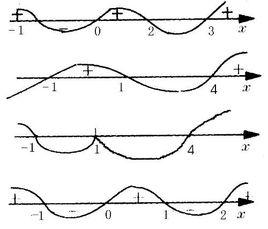
釋義
“穿針引線法”又稱“ 數軸穿根法”或“ 數軸標根法”。
準確的說，應該叫做“序軸標根法”。序軸：省去原點和單位，只表示數的大小的數軸。序軸上標出的兩點中，左邊的點表示的數比右邊的點表示的數小。
當高次不等式f（x）>0（或<0）的左邊整式、分式不等式φ（x）/h（x）>0（或<0）的左邊分子、分母能分解成若干個一次因式的積（x－a1）（x－a2）…（x－an）的形式，可把各因式的根標在數軸上，形成若干個區間，最右端的區間f（x）、 φ（x）/h（x）的值必為正值，從右往左通常為正值、負值依次相間，這種解不等式的方法稱為序軸標根法。
為了形象地體現正負值的變化規律，可以畫一條浪線 從右上方依次穿過每一根所對應的點， 穿過最後一個點後就不再變方向，這種畫法俗稱“ 穿針引線法“。
用途
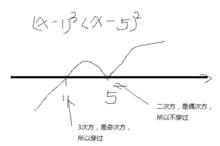穿針引線法解高次不等式用於解簡單高次不等式。
發明者
淮南三中一名老教師。於1983發表的一篇論文《數軸標根法解不等式》上介紹此法，便於解此類不等式。
用法
當高次不等式f（x）>0（或<0）的左邊整式、分式不等式φ（x）/h（x）>0（或<0）的左邊分子、分母能分解成若干個一次因式的積（x－a1）（x－a2）…（x－an）的形式，可把各因式的根標在數軸上，形成若干個區間，最右端的區間f（x）、 φ（x）/h（x）的值必為正值，從右往左通常為正值、負值依次相間，這種解不等式的方法稱為序軸標根法。
為了形象地體現正負值的變化規律，可以畫一條浪線從右上方依次穿過每一根所對應的點，穿過最後一個點後就不再變方向，這種畫法俗稱“穿針引線法“。
使用步驟
第一步
通過不等式的諸多性質對不等式進行移項，使得右側為0。（注意：一定要保證最高次數項的係數為正數）
例如：將x^3-2x^2-x+2>0化為(x-2)(x-1)(x+1)>0
第二步
將不等號換成等號解出所有根。
例如：(x-2)(x-1)(x+1)=0的根為：x1=2，x2=1，x3=-1
第三步
在數軸上從左到右按照大小依次標出各根。
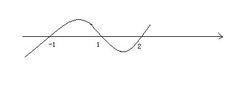奇穿偶不穿例如：-1 1 2
第四步
畫穿根線：以數軸為標準，從“最右根”的右上方穿過根，往左下畫線，然後又穿過“次右根”上去，一上一下依次穿過各根。
第五步
觀察不等號，如果不等號為“>”，則取數軸上方，穿根線以內的範圍；如果不等號為“<”，則取數軸下方，穿根線以內的範圍。
例如：
若求(x-2)(x-1)(x+1)>0的根。
在數軸上標根得：-1 1 2
畫穿根線：由右上方開始穿根。
因為不等號為“>”則取數軸上方，穿根線以內的範圍。即：-1<x<1或x>2。
奇穿偶不穿：即假如有兩個解都是同一個數字。這個數字要按照兩個數字穿。如（x-1)^2=0 兩個解都是1 ，那么穿的時候不要透過1
可以簡單記為秘籍口訣：或“ 自上而下，從右到左，奇穿偶不穿”（也可以這樣記憶：“自上而下，自右而左，奇穿偶回” 或“奇穿偶連”）。
注意事項
運用 序軸標根法解不等式時，常犯以下的錯誤：
問題一
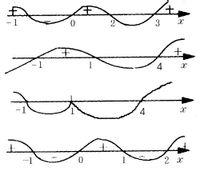穿針引線法出現形如（a－x）的一次因式時，勿匆忙地“穿針引線”。
例1 解不等式x（3－x）（x+1）（x－2）>0。
解 x（3－x）（x+1）（x－2）>0，將各根－1、0、2、3依次標在數軸上，由圖1可得原不等式的解集為{x|x<－1或0<x<2或x>3}。
事實上，只有將因式（a－x）變為（x－a）的形式後才能用序軸標根法，正確的解法是：
【解】原不等式變形為x（x－3）（x+1）（x－2）<0，將各根－1、0、2、3依次標在數軸上，由圖1，原不等式的解集為{x|－1<x<0或2<x<3}。
問題二
出現重根時，機械地“穿針引線”。
例2 解不等式（x+1）（x－1）^2（x－4）^3<0
解 將三個根－1、1、4標在數軸上，
原不等式的解集為{x|x<－1或1<x<4}。
這種解法也是錯誤的，錯在不加分析地、機械地“穿針引線”。出現幾個相同的根時，所畫的浪線遇到“偶次”點（即偶數個相同根所對應的點）不能過數軸，仍在數軸的同側折回，只有遇到“奇次”點（即奇數個相同根所對應的點）才能穿過數軸，正確的解法如下：
解 將三個根－1、1、4標在數軸上，畫出浪線圖來穿過各根對應點，遇到x=1的點時浪線不穿過數軸，仍在數軸的同側折回；遇到x=4的點才穿過數軸，於是，可得到不等式的解集
{x|－1<x<4且x≠1}
問題三
出現不能再分解的二次因式時，簡單地放棄“穿針引線”
例3 解不等式x（x+1）（x－2）（x^3－1）>0
解 原不等式變形為x（x+1）（x－2）（x－1）（x^2+x+1）>0，有些同學同解變形到這裡時，認為不能用序軸標根法了，因為序軸標根法指明要分解成一次因式的積，事實上，根據這個二次因式的符號將其消去，再運用序軸標根法即可。
解 原不等式等價於
x（x+1）（x－2）（x－1）（x^2+x+1）>0，
∵ x^2+x+1>0對一切x恆成立，
∴ x（x－1）（x+1）（x－2）>0，由圖4可得原不等式的解集為{x|x<－1或0<x<1或x>2}
