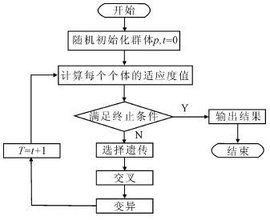
程式算法:程式算法是對特定問題求解過程的描述，是指令的有限序列，每條指令 -百科知識中文網

什麼是程式算法？

程式算法是對特定問題求解過程的描述，是指令的有限序列，每條指令完成一個或多個操作。通俗地講，就是為解決某一特定問題而採取的具體有限的操作步驟。

（1）有窮性：在有限的操作步驟內完成。有窮性是算法的重要特性，任何一個問題的解決不論其採取什麼樣的算法，其終歸是要把問題解決好。如果一種算法的執行時間是無限的，或在期望的時間內沒有完成，那么這種算法就是無用和徒勞的，我們不能稱其為算法。

（2）確定性：每個步驟確定，步驟的結果確定。算法中的每一個步驟其目的應該是明確的，對問題的解決是有貢獻的。如果採取了一系列步驟而問題沒有得到徹底的解決，也就達不到目的，則該步驟是無意義的。

（3）可行性：每個步驟有效執行，得到確定的結果。每一個具體步驟在通過計算機實現時應能夠使計算機完成，如果這一步驟在計算機上無法實現，也就達不到預期的目的，那么這一步驟是不完善的和不正確的，是不可行的。

（4）零個或多個輸入：從外界獲得信息。算法的過程可以無數據輸入，也可以有多種類型的多個數據輸入，需根據具體的問題加以分析。

（5）一個或多個輸出：算法得到的結果就是算法的輸出（不一定就是列印輸出）。算法的目的是為解決一個具體問題，一旦問題得以解決，就說明採取的算法是正確的，而結果的輸出正是驗證這一目的的最好方式。

同一問題可用不同算法解決，而一個算法的質量優劣將影響到算法乃至程式的效率。算法分析的目的在於選擇合適算法和改進算法。一個算法的評價主要從時間複雜度和空間複雜度來考慮。

算法的時間複雜度是指算法需要消耗的時間資源。一般來說，計算機算法是問題規模n 的函式f(n)，算法的時間複雜度也因此記做

T(n)=Ο(f(n))

因此，問題的規模n 越大，算法執行的時間的增長率與f(n) 的增長率正相關，稱作漸進時間複雜度（Asymptotic Time Complexity）。

算法的空間複雜度是指算法需要消耗的空間資源。其計算和表示方法與時間複雜度類似，一般都用複雜度的漸近性來表示。同時間複雜度相比，空間複雜度的分析要簡單得多。