基本介紹
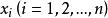 科克倫定理
科克倫定理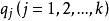 科克倫定理
科克倫定理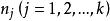 科克倫定理
科克倫定理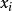 科克倫定理
科克倫定理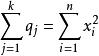 科克倫定理
科克倫定理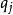 科克倫定理
科克倫定理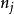 科克倫定理
科克倫定理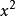 科克倫定理
科克倫定理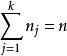 科克倫定理
科克倫定理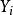 科克倫定理
科克倫定理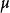 科克倫定理
科克倫定理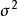 科克倫定理
科克倫定理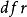 科克倫定理
科克倫定理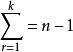 科克倫定理
科克倫定理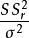 科克倫定理
科克倫定理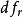 科克倫定理
科克倫定理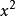 科克倫定理
科克倫定理如果 是獨立的標準常態分配的變數, 為具有秩 的變數 的二次式。如果 ,那么 為獨立的自由度分別為 的 變數的充分必要條件是 。這一定理套用到回歸分析中,如果 的n個觀察值均來自同樣的均值為 ,方差為 的常態分配,SSTO是總的離差平方和,自由度為n-1可分解成K個平方和SS,其自由度分別為 ,如果 ,那么 項分別是自由度為 的 變數 。
線上性統計推斷中,科克倫(Cochran)定理及其推廣形式發揮著重要的作用,它主要研究獨立正態隨機變數的二次型函式的性質。
科克倫定理及其證明
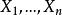 科克倫定理
科克倫定理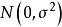 科克倫定理
科克倫定理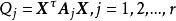 科克倫定理
科克倫定理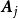 科克倫定理
科克倫定理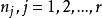 科克倫定理
科克倫定理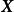 科克倫定理
科克倫定理科克倫定理 設隨機變數 相互獨立,且都服從常態分配 ,記 ,其中 是n階非負定的對稱陣,且其秩為 , 又是隨機(列)向量
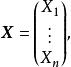 科克倫定理
科克倫定理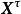 科克倫定理
科克倫定理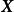 科克倫定理
科克倫定理 科克倫定理
科克倫定理表示 的轉置 。如果
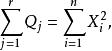 科克倫定理
科克倫定理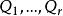 科克倫定理
科克倫定理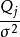 科克倫定理
科克倫定理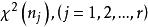 科克倫定理
科克倫定理那么, 相互獨立且 服從 的充分必要條件是
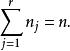 科克倫定理
科克倫定理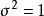 科克倫定理
科克倫定理證明 不失一般性,假定,不然的話,可以先令
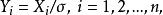 科克倫定理
科克倫定理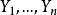 科克倫定理
科克倫定理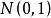 科克倫定理
科克倫定理這時,相互獨立,且都服從。
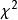 科克倫定理
科克倫定理由分布的可加性立即可以推得必要性成立,下面證明充分性。
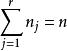 科克倫定理
科克倫定理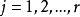 科克倫定理
科克倫定理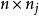 科克倫定理
科克倫定理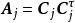 科克倫定理
科克倫定理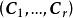 科克倫定理
科克倫定理假定成立,對每一個,由於 A是n階非負定的方陣,因此由線性代數理論知道,存在秩為n的矩陣 C,使得把分塊矩陣記作 C。易見, C是n階方陣。作變換
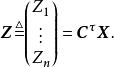 科克倫定理
科克倫定理由
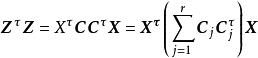 科克倫定理
科克倫定理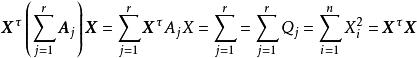 科克倫定理
科克倫定理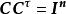 科克倫定理
科克倫定理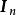 科克倫定理
科克倫定理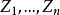 科克倫定理
科克倫定理推知,這裡表示n階單位陣.這表明 C是正交陣。因此,是相互獨立的隨機變數,且都服從N(0,1),注意到(n理解為0)
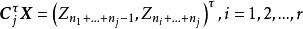 科克倫定理
科克倫定理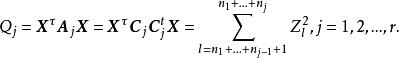 科克倫定理
科克倫定理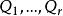 科克倫定理
科克倫定理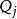 科克倫定理
科克倫定理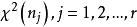 科克倫定理
科克倫定理這表明相互獨立且服從。

