定義
定義一
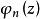 漸近展開
漸近展開漸近展開是函式的級數展開的推廣。設{ }是z→z0時的漸近序列,如果對每一個自然數N有
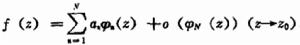 漸近展開
漸近展開其中αn是常數,則稱
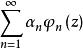 漸近展開
漸近展開是f(z)的漸近展開式,並記為
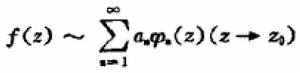 漸近展開
漸近展開當漸近序列指定的條件下,一個函式的漸近展開式是唯一i確定的,它的展開係數αn按如下公式來求得:
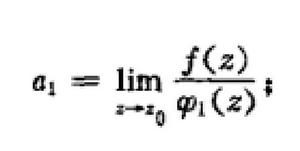 漸近展開
漸近展開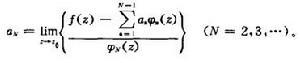 漸近展開
漸近展開漸近展開被定義為一個函式級數(通常是柯西發散的),該級數的每一個部分和都給出該函式的一個漸近表達式。
定義二
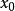 漸近展開
漸近展開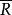 漸近展開
漸近展開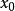 漸近展開
漸近展開設P為 R的子集, 為接觸於P的 的點,ξ為 之鄰域上的比較尺度,ψ為ξ的元素,而f為定義在P上、在賦范向量空間F中取值的映射.則至多存在一個具有限支集的F的元素族
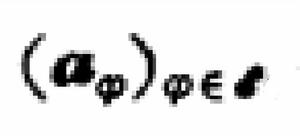 漸近展開
漸近展開使,
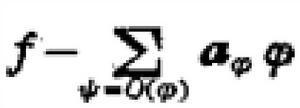 漸近展開
漸近展開對於ψ來說是可忽略的;映射
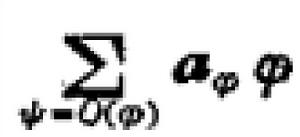 漸近展開
漸近展開叫做f以Ψ為精確度的漸近展開.
拉普拉斯 積分的漸近展開
構造拉普拉斯積分的漸近展開的拉普拉斯方法.這個方法是拉普拉斯在研究機率論的極限理論時發現的,它是後來由黎曼發展起來的漸近分析理論的主要組成部分,通常在複分析教程中有這方面內容的敘述.各種漸近分析方法的進一步的知識可在在參考文獻中獲得.
與一般級數展開的區別
粗略來說,漸近級數與一般的級數展開(例如泰勒級數)的區別在於,漸近級數是z越接近z,部分和越接近被展開的函式,而泰勒級數等則是z點固定,取的項數越多結果越接近被展開的函式。
另外一個重要的區別是,漸近展開常常需要對宗量有額外的限制,例如輻角的限制。
除此之外,一個函式在一點的泰勒展開表達式確定了以該點為中心的收斂圓內函式的形式,而漸近級數則不然,詳見下一小節的討論。
