沃利斯乘積

沃利斯乘積是約翰·沃利斯提出的一個有名的數學公式。

定義

數學家約翰·沃利斯在1655年寫下了今日有名的 沃利斯乘積

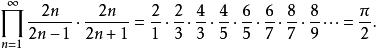沃利斯乘積

當時證明

今日多數的微積分教科書透過比較{\displaystyle \int _{0}^{\pi }\sin ^{n}xdx}在 n是奇數或是偶數，甚至是接近無窮大的情況下，發現即使將 n增加一就會發生不一樣的情形。在那時，微積分尚未存在，而且有關數學收斂的分析工具也還未俱全，所以完成這證明較現今有相當的難度。從現在來看，從歐拉公式中的正弦展開式得到此乘積是必然的結果。

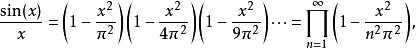沃利斯乘積

在 x= π/2時

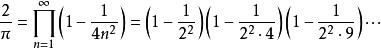沃利斯乘積

嚴謹證明

先考慮不定積分{\displaystyle \int \sin ^{n}xdx}有

沃利斯乘積

故

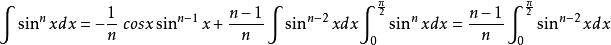沃利斯乘積

對整數m

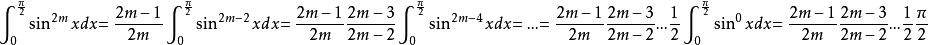沃利斯乘積

另一方面

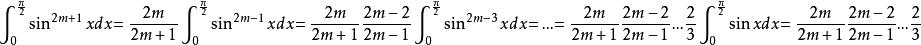沃利斯乘積

兩式相除得

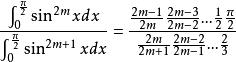沃利斯乘積

故

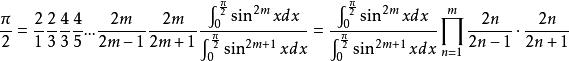沃利斯乘積

又因為

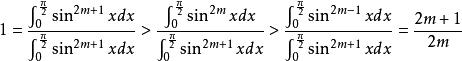沃利斯乘積

由夾擠定理知

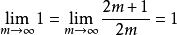沃利斯乘積

故

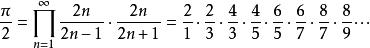沃利斯乘積

尋找 ζ(2)

我們可將上述的正弦乘積式化為泰勒級數：

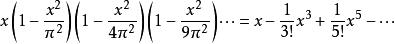沃利斯乘積