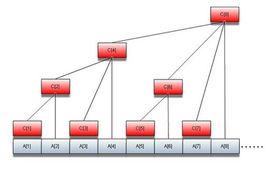
樹狀圖概念
假設數組a[1..n]，那么查詢a[1]+...+a[n]的時間是log級別的，而且是一個線上的數據結構，支持隨時修改某個元素的值，複雜度也為log級別。
來觀察這個圖：
令這棵樹的結點編號為C1，C2...Cn。令每個結點的值為這棵樹的值的總和，那么容易發現：
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
這裡有一個有趣的性質：
設節點編號為x，那么這個節點管轄的區間為2^k（其中k為x二進制末尾0的個數）個元素。因為這個區間最後一個元素必然為Ax，
所以很明顯：Cn = A(n – 2^k + 1) + ... + An
算這個2^k有一個快捷的辦法，定義一個函式如下即可：
利用機器補碼特性，也可以寫成：
當想要查詢一個SUM(n )(求a[n]的和），可以依據如下算法即可：
step1: 令sum = 0，轉第二步；
step2: 假如n <= 0，算法結束，返回sum值，否則sum = sum + Cn，轉第三步；
step3: 令n = n – lowbit(n)，轉第二步。
可以看出，這個算法就是將這一個個區間的和全部加起來，為什麼是效率是log(n)的呢？以下給出證明：
n = n – lowbit(n)這一步實際上等價於將n的二進制的最後一個1減去。而n的二進制里最多有log(n)個1，所以查詢效率是log(n)的。
那么修改呢，修改一個節點，必須修改其所有祖先，最壞情況下為修改第一個元素，最多有log(n)的祖先。
所以修改算法如下（給某個結點i加上x）：
step1: 當i > n時，算法結束，否則轉第二步；
step2: Ci = Ci + x， i = i + lowbit(i)轉第一步。
i = i +lowbit(i)這個過程實際上也只是一個把末尾1補為0的過程。
對於數組求和來說樹狀數組簡直太快了!
註：
求lowbit(x)的建議公式：
lowbit(x):=x and -x;
或lowbit(x):=x and (x xor (x - 1));
lowbit(x)即為2^k的值。
充分性
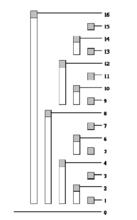樹狀數組線性圖很容易知道C8表示A1～A8的和，但是C6卻是表示A5～A6的和，為什麼會產生這樣的區別的呢？或者說發明她的人為什麼這樣區別對待呢？
答案是，這樣會使操作更簡單！看到這相信有些人就有些感覺了，為什麼複雜度被log了呢？可以看到，C8可以看作A1～A8的左半邊和+右半邊和，而其中左半邊和是確定的C4，右半邊其實也是同樣的規則把A5～A8一分為二……繼續下去都是一分為二直到不能分樹狀數組巧妙地利用了二分，樹狀數組並不神秘，關鍵是巧妙！
代碼實現
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | template<typenamename,intlen>structbinary_indexed_tree { namec[len]; voidclear() { memset(c,0,sizeof(c)); } voidadd(intdep,namevalue) { for(;dep<=len;dep+=lowbit(dep))c[dep]+=value; } voidchange(intdep,namevalue) { add(dep,value+c[dep-1]-c[dep]); } nameprefix(intdep) { intsum=0; for(;dep;dep-=lowbit(dep))sum+=c[dep]; returnsum; } namesum(intl,intr) { returnprefix(r)-prefix(l-1); } }; |
典題分析
例題1
給定一個初始值都為0的序列,動態地修改一些位置上的數字,加上一個數,減去一個數,或者乘上一個數,然後動態地提出問題,問題的形式是求出一段數字的和.
算法分析
如果直接做的話,修改的複雜度是O(1),詢問的複雜度是O(N),M次詢問的複雜度是M*N.M,N的範圍可以有100000以上,所以這樣做會逾時,但是如果用線段樹的話,還是很不錯的! 有很多線段樹能實現但樹狀數組卻實現不了的題目。
線段樹解法分析
可以看出,這棵樹的構造用二分便可以實現.複雜度是2*N.
每個結點用數組a來表示該結點所表示範圍內的數據之和.
修改一個位置上數字的值,就是修改一個葉子結點的值,而當程式由葉子結點返回根節點的同時順便修改掉路徑上的結點的a數組的值.
對於詢問的回答,可以直接查找i..j範圍內的值,遇到分叉時就兵分兩路,最後在合起來.也可以先找出0..i-1的值和0..j的值,兩個值減一減就行了.後者的實際操作次數比前者小一些.
這樣修改與維護的複雜度是logN.詢問的複雜度也是logN,對於M次詢問,複雜度是MlogN.
然而不難發現,線段樹的編程複雜度大,空間複雜度大,時間效率也不高!!!!
所以我們來想用樹形數組來實現:
那么,何為樹形數組呢??
C數組就是樹狀數組,a數組是原數組;
對於序列a，我們設一個數組C定義C[t] = a[t – 2^k + 1] + … + a[t]，k為t在二進制下末尾0的個數。
K的計算可以這樣:
2^k=t and (t xor (t-1))
以6為例
(6)10=(0110)2
xor 6-1=(5)10=(0101)2
(0011)2
and (6)10=(0110)2
(0010)2
所以問題變的很簡單,重要寫幾個函式就可以了;
求2^k的函式代碼如下:
求1 -- end和的函式代碼如下:
對某位進行操作函式如下(以加法為例)
有了這三個函式整個樹形數組也就基本構建成功啦!!
對於剛才的一題,每次修改與詢問都是對C數組做處理.空間複雜度有3N降為N,時間效率也有所提高.編程複雜度更是降了不少.
對於lowbit可有最佳化 P :lowbit:=X AND(not x+1){或 X AND (-X)}; C: lowbit:=x &(-x){或 x & (~x+1)};
例題2
求n個數中 k組提問 從t到t1個數字之和
pascal代碼
線段樹的比較
樹狀數組是一個可以很高效的進行區間統計的數據結構。在思想上類似於線段樹，比線段樹節省空間，編程複雜度比線段樹低，但適用範圍比線段樹小。
以簡單的求和為例。設原數組為a[1..N]，樹狀數組為c[1..N]，其中c[k] = a[k-(2^t)+1] + ... + a[k]。比如c[6] = a[5] + a[6]。也就是說，把k表示成二進制1***10000，那么c[k]就是1***00001 + 1***00010 + ... + 1***10000這一段數的和。設一個函式lowestbit(k)為取得k的最低非零位，容易發現，根據上面的表示方法，從a[1]到a[k]的所有數的總和即為sum[k] = c[k] + c[k-lowestbit(k)] + c[k-lowestbit(k)-lowestbit(k-lowestbit(k))] + ... 於是可以在logk的時間內求出sum[k]。當數組中某元素髮生變化時，需要改動的c值是c[k],c[k+lowestbit(k)], c[k+lowestbit(k)+lowestbit(k+lowestbit(k))] ... 這個複雜度是logN (N為最大範圍)
擴展到多維情況：以二維為例，用c[k1][k2]表示c[k1-(2^t1)+1][k2-(2^t2)+1] + ... + c[k1][k2]的總和。可以用類似的方法進行處理。複雜度為(logn)^k (k為維數)
樹狀數組相比線段樹的優勢：空間複雜度略低，編程複雜度低，容易擴展到多維情況。劣勢：適用範圍小，對可以進行的運算也有限制，比如每次要查詢的是一個區間的最小值，似乎就沒有很好的解決辦法。
多維情況的幾道題目:
URAL 1470 UFOs
POJ 2155 Matrix
表面上看，這題的要求似乎和樹狀數組的使用方法恰好相反，改變的是一個區間，查詢的反而是一個點。實際上可以通過一個轉化巧妙的解決。
首先對於每個數A定義集合up(A)表示{A, A+lowestbit(A), A+lowestbit(A)+lowestbit(A+lowestbit(A))...} 定義集合down(A)表示{A, A-lowestbit(A), A-lowestbit(A)-lowestbit(A-lowestbit(A)) ... , 0}。可以發現對於任何A<B，up(A)和down(B)的交集有且僅有一個數。
於是對於這道題目來說，翻轉一個區間[A,B]（為了便於討論先把原問題降為一維的情況），我們可以把down(B)的所有元素的翻轉次數+1，再把down(A-1)的所有元素的翻轉次數-1。而每次查詢一個元素C時，只需要統計up(C)的所有元素的翻轉次數之和，即為C實際被翻轉的次數。
實際實現時，由於只考慮奇偶，因此無須統計確切的翻轉次數。另外，如果翻轉up(A)和up(B+1)，查詢down(C)，也是同樣的效果。這種方法可以很容易地擴展到二維情況。比起線段樹、四分樹之類的常規思路，無論編程複雜度還是常數速度上都有很大優勢。
