基本了解
由於標準數獨的難度差異較大,故按照難度,分為主要技巧、中級技巧、高級技巧、頂級技巧等。
主要技巧是指,基本入門、或常規大賽之中,經常需要使用到的技巧。它包含 排除(另稱“摒除法”或“隱性唯一”)、 唯一餘數(另稱“顯性唯一”,簡稱“唯余”)、 顯性數對(另稱“唯餘數對”或“數對唯余法”)、 隱性數對(另稱“排除數對”或“數對占位法”)、 區塊排除等,及其他們複合使用的技巧,比如 區塊唯一餘數。此處僅研究和表述標準數獨使用的技巧。
因為技巧較多,所以非主要技巧者,均以外鏈形式為您展示。本文僅介紹主要技巧。
註:本文不包括變型數獨技巧,比如鋸齒數獨的 割補法(縮寫LoL)、殺手數獨的 45法則(另稱“45定則”)等。複合使用技巧在技巧研究之中被等效分解為多個步驟,因此僅出現於大賽和平時練習之中。
在進入技巧了解前,您需要了解數獨的基本規則和常用術語名稱。
標準數獨規則
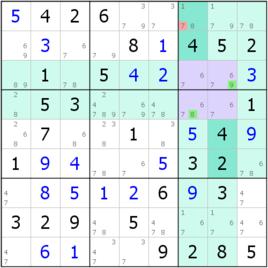
在空格內填入1~9的任意一個數,使得盤面內,每一行、每一列、每一個正方形粗線九宮格區域內的數字,均包含1到9,不含有重複的數字。
基本數獨術語
| 行(Row):數獨盤面之中,每一個橫排。比如圖中塗藍色的9個單元格組,共同構成一行。標準數獨盤面一共含有9行。 一般我們記每一行為“r幾”(字母 r 不區分大小寫),比如第4行記作“r4”。 | 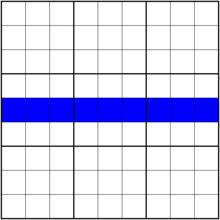 r5 r5 |
| 列(Column):數獨盤面之中,每一個豎列。比如圖中塗藍色的9個單元格組,共同構成一列。標準數獨盤面一共含有9列。 一般我們記每一行為“c幾”(字母 c 不區分大小寫),比如第4行記作“c4”。 | 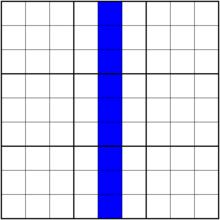 c5 c5 |
| 宮(Block):數獨盤面之中,每一個正方形的、用粗線圍住的九宮格。比如圖中塗藍色的9個單元格組,共同構成一個宮。標準數獨盤面一共含有9個宮。 一般我們記每一宮為“b幾”(字母 b 不區分大小寫),比如第3宮記作“b3”。 | 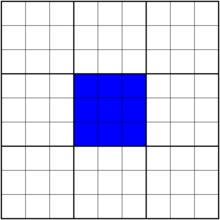 b5 b5 |
| 單元格(Cell):數獨盤面之中,每一個小的格子。標準數獨一共含有81個單元格。 一般我們用“r幾c幾”表示每一個單元格,比如第3行第7格記作“r3c7”。 | 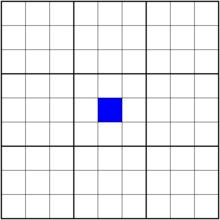 r5c5 r5c5 |
| 相關格組(Peer):每一個單元格所在的行、列、宮內的其餘單元格的集合。此術語一般用於討論性技巧之中。也稱等位群格位。 | 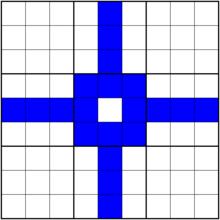 r5c5的相關格組 r5c5的相關格組 |
| 提示數(Hint):數獨要求每一個題目都只能有一個答案,即每一個單元格上都只有一種填數的可能情況(這被稱為題目唯一解)。於是為了保證唯一解,在最開始就必須給定一部分位置的數字用於推理和推導填數,直至完成盤面。這些數字被稱為提示數。也被稱為 已知數。 | |
| 明數(Value):在一個已經完成了一部分的盤面內,所有提示數和自行推導得到的填入的數字,統稱明數。其中自行推導得到的填入的數字稱為 填數。 | |
| 候選數(Candidate):每一個單元格的所有填數情況。也稱 暗數。 | |
| 出數:得到填數的結論。 | |
| 刪數:得到刪除候選數的結論。 |
其他的數獨相關術語名詞請查看數獨術語。以下將為您介紹主要技巧的使用。
主要技巧
排除(Hidden Single)
排除法(或叫摒除法)按照行列宮的不同,分三種類型。
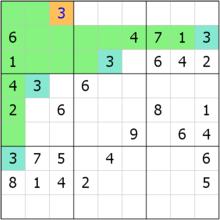 b1排除 b1排除 | 根據數獨規則,我們可以觀察到,數字3在b1內只有唯一的一個位置可以填,就是r1c3。由於c1、c2中已經出現了3,並且b2、b3也出現了3,所以在b1內,3的位置將不得出現在r1c1、r1c2、r2c2、r2c3、r3c2、r3c3這6格。而由於b1內必須出現數字3,所以只能填入r1c3處。因此,r1c3=3。 |
 c1排除 c1排除 | 我們可以觀察到,在c1中,數字3的位置僅僅只能填在c1的r8c1處,因為c1內有6個空格,提示數3的位置使得r1c1、r2c1、r3c1、r5c1和r9c1這5格不得填入3,因此3被理所當然地“框”在了r8c1處。所以r8c1=3。 |
唯一餘數(Naked Single)
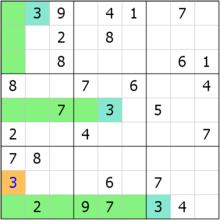
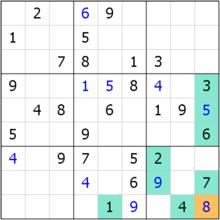 r9c9唯余
r9c9唯余r9c9的相關格組分別在r9,c9和b9,於是就看這三個部分,我們發現一共出現了1、9、4、3、5、6、7、2這些數字。根據摒除法的規則,r9c9的位置將不得填入它們。神奇的是,在這九個數字中,單單只有8沒出現。根據我們在之前的摒除法中推出的東西,即“1~9的每個數字都要出現一次”,得到結論,r9c9=8。
唯一餘數法,簡稱唯余法,是一種某個單元格中被摒除法排除情況後,只剩下1~9的其中某個數字沒有填,從而得到它就是此單元格的值的解法。唯一餘數法也可以適用於僅在同一個單元內部的推理,中文稱之為 點算法(Full House)。
當全盤具有候選數的時候,唯余法將變得很好觀察:只要某一個單元格內只有1個候選數的時候,它就是這個單元格的值,這就是唯余法。普通點算需要自己多加練習,速度提高才能靈活使用和觀察到。
區塊排除(Locked Candidates)
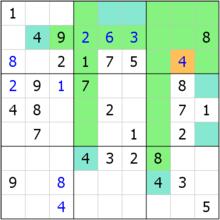 區塊排除
區塊排除我們發現在b2中,4的位置無論是在r1c5還是r1c6,都恰好在r1。但是無論怎么說,這兩個位置都必須有一個數字填入4,因此r1的其餘位置都不能填4。r4c9和r6c9同理。此時我們發現,b3僅僅只有r3c8可以填4。所以r3c8=4。
這種技巧被稱為區塊摒除法,用區塊排除了行和列的,稱為 宮對行列區塊摒除法(Pointing);而下面這個例子則為 行列區塊對宮摒除法(Claiming);而它們各自構成一個 區塊(Intersection),例如,單元格組{r1c5, r1c6}就構成一個區塊。
區塊唯一餘數(Intersected Naked Single)
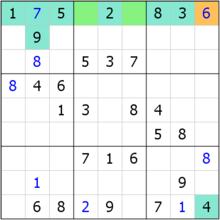 r1c9區塊唯余
r1c9區塊唯余區塊唯一餘數是帶有區塊的唯一餘數技巧。簡稱 區塊唯余。
我們發現,b2填9的位置,被r2c2(9)排除影響,導致最終只剩下r1c4和r1c6可以填9。由於單元格組{r1c4, r1c6}同一行,所以形成區塊。根據唯一餘數的理解,我們能夠得到r1c9={69}。而r1存在一個區塊,因此不允許再有第二個9的出現,故r1c9=6。
顯性數對(Naked Pair)
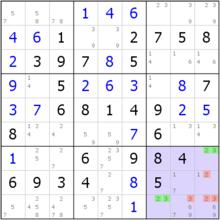 {23}數對唯余
{23}數對唯余我們看b9,此時發現r7c9和r9c7這2格的候選數都是2和3(利用摒除法排除掉候選數)。這2個單元格剛好可以放下這兩個數字,要么r7c9=2、r9c7=3;要么r7c9=3、r9c7=2,而且也就只有這兩種情況。無論是其中的哪種情況,b9內的其他位置都不得填2和3了,因為,它們恰好都在b9。因此,可以直接刪除掉r8c9(2)、r9c8(3)、r9c9(2, 3)(r8c8(2, 3)已經被r5c8(2)以及r8c3(3)排除掉了)。此時,我們就稱r7c9和r9c7內的候選數2和3構成數對結構。
隱性數對(Hidden Pair)
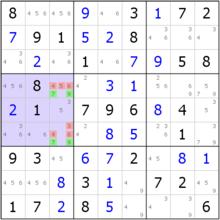 {79}數對占位
{79}數對占位在b4中,數字7和9可以出現的位置只剩下r4c3和r6c3。摒除後發現剛好在b4內只有2格可以填入7和9這兩個數字。然而,這剛好滿足數對的定義,所以可以排除這個格子內的其餘填數情況將全部排除。因此,我們可以得到:r4c3<>{456}、r6c3<>{346},即r4c3, r6c3={79}。
很顯然,{79}數對將r4c3和r6c3的其他情況全“排擠”開了,因此,這種解法就被稱為“數對的‘占位’法”。這裡的占位就能形象地詮釋了排擠的意思,這也被稱為 數對占位法。
非主要技巧匯總
本節將展示所有標準數獨技巧的名稱。
| 技巧類型 | 標準技巧名 | 詳細技巧分類 |
| 基本技巧 | 排除 | 宮排除 |
| 行排除 | ||
| 列排除 | ||
| 區塊 | 宮區塊對行列排除 | |
| 行列區塊對宮排除 | ||
| 唯一餘數 | 單區唯余(點算) | |
| 多區唯余 | ||
| 區塊唯余 | ||
| 數組 | 標準數組 | 顯性數組 |
| 隱性數組 | ||
| 死鎖數組 | ||
| 魚(形狀變異) | 標準魚 | |
| 宮內魚 | ||
| 交叉魚 | ||
| 魚(帶鰭變異) | 外鰭魚 | 外鰭標準魚 |
| 外鰭宮內魚 | ||
| 外鰭交叉魚 | ||
| 外鰭退化魚(退化魚) | 退化標準魚 | |
| 退化宮內魚 | ||
| 退化交叉魚 | ||
| 內鰭魚 | 內鰭宮內魚 | |
| 內鰭交叉魚 | ||
| 自噬鰭魚 | 自噬宮內魚 | |
| 自噬交叉魚 | ||
| 過飽和魚 | ||
| 匹配法 | 規則匹配法(分支匹配法) | |
| 不規則匹配法 | 首尾數對匹配法(W-Wing) | |
| 隔一數對匹配法(M-Wing) | ||
| 分裂匹配法(Split-Wing/S-Wing) | ||
| 拐角匹配法(Local-Wing/L-Wing) | ||
| 雜合匹配法(Hybrid-Wing/H-Wing) | ||
| 致命結構 | 雙值格致命結構 | 唯一矩形 |
| 唯一環 | ||
| 拓展矩形 | ||
| 全盤雙值格致死解法 | ||
| 複雜雙值格致命結構 | ||
| 多值格致命結構 | 致命多邊形 | |
| 複雜致命結構 | ||
| 明數致命結構 | 可規避矩形 | |
| 可規避全局數對 | ||
| 反用局部唯一 | ||
| 其他致命結構 | 宇宙法 | |
| 枚舉法 | 多格枚舉法 | |
| Subset Counting | ||
| 待定數組 | 區塊性待定數組 | 欠一數組 |
| 非區塊性待定數組 | 融合式待定數組 | |
| 偽數組 | ||
| 融合式待定數組拓展 | 復融合式待定數組 | |
| 多米諾鏈 | ||
| 多米諾環 | ||
| 鏈性待定數組 | 雙強法則待定數組鏈(ALS-XZ) | |
| 三強法則待定數組鏈(ALS-XY-Wing) | ||
| 多強法則待定數組鏈(ALS-XY-Chain) | ||
| 死亡綻放(Death Blossom) | ||
| 首尾數對待定數組鏈(ALS-W-Wing) | ||
| 塗色法 | 同數塗色法 | 色鏈 |
| 色分 | ||
| 異數塗色法 | 進階塗色(三維美杜莎) | |
| 代數法(袋鼠) | ||
| 鏈 | 同數鏈 | 摩天樓 |
| 雙線風箏 | ||
| 多寶魚(雙強鏈) | ||
| 守護者 | ||
| 異數鏈 | 二元鏈(雙值格鏈)(XY-Chain/Y-Chain) | |
| 遠程數對 | ||
| 不連續環 | ||
| 首尾異數鏈 | ||
| 超鏈 | 區塊鏈 | |
| 鏈置候選數技巧 | ||
| 強制鏈 | 矛盾強制鏈組 | |
| 分類強制鏈組 | ||
| 動態鏈 | ||
| 構造鏈 | 毛刺 | |
| 毛邊 | ||
| 環 | ||
| 魚雷 | 初級魚雷 | 初級標準魚雷 |
| 初級宮內魚雷 | ||
| 初級交叉魚雷 | ||
| 高級魚雷 | 高級標準魚雷 | |
| 高級宮內魚雷 | ||
| 高級交叉魚雷 | ||
| 網 | 標準網 | |
| 形狀變異網 | 宮區域網路 | |
| 交叉網 |
您也可以參考外國文獻學習標準數獨技巧。