復倒譜

復倒譜是一個函式的傅立葉變換的對數的傅立葉反變換。對褶積信號的線性分離作用，在實際信號處理中很有用處。

復倒譜

正文

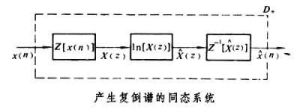
一個函式的傅立葉變換的對數的傅立葉反變換。對褶積信號的線性分離作用，在實際信號處理中很有用處，例如可套用於通信、建築聲學、地震分析、地質勘探和語音處理等領域。尤其在語音處理方面，套用復倒譜算法可製成同態預測聲碼器系統，用於高度保密的通信。
在離散信號x(n)情況下，用z變換表示復倒譜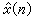，可以寫作

復倒譜可以利用同態系統中一種特定的特徵系統來求得，如圖所示。為了區別於用一般方法所求得的頻譜(spectrum)，將spectrum這一詞前半部(spec)字母順序顛倒即成cepstrum，根據詞形定名為倒譜。又因頻譜一般為複數譜，故稱為復倒譜。為了說明復倒譜的性質,假設已知兩信號x1(n)和x2(n)相褶積而得到的時間函式x(n)，對它們分別求其離散傅立葉變換，寫作

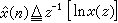
X(ω)＝DFT【x(n)】　 X1(ω)＝DFT【x1(n)】

X2(ω)＝DFT【x2(n)】

按上述定義，可得到如下關係式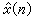

＝IDFT｛log【X(ω)】｝
＝IDFT｛log【X1(ω)】｝＋IDFT｛log【X2(ω)】｝

由此可見,通過復倒譜的運算可將x1(n)和x2(n)的褶積關係變換為相加關係，再採用一般線性系統對它們進行濾波處理。

復倒譜

配圖

相關連線