近似
從頭計算法中引入的近似很少，主要包括
•玻恩–奧本海默近似
•單電子近似
•非相對論近似
對於具體的方法而言，可能用到其中的一種或幾種近似。
玻恩–奧本海默近似
玻恩–奧本海默近似（Born-Oppenheimer approximation，簡稱 BO近似，又稱 絕熱近似）是一種普遍使用的解包含電子與原子核的體系的量子力學方程的近似方法。
在用量子力學處理分子或其他體系時，需要通過解薛定鍔方程或其他類似的偏微分方程獲得體系波函式。這個過程往往由於體系自由度過多而非常困難，甚至無法進行。據玻恩－奧本海默近似中，考慮到原子核的質量要比電子大很多，一般要大3-4個數量級，因而在同樣的相互作用下，電子的移動速度會較原子核快很多，這一速度的差異的結果是使得電子在每一時刻仿佛運動在靜止原子核構成的勢場中，而原子核則感受不到電子的具體位置，而只能受到平均作用力。由此，可以實現原子核坐標與電子坐標的近似變數分離，將求解整個體系的波函式的複雜過程分解為求解電子波函式和求解原子核波函式兩個相對簡單得多的過程。
在玻恩－奧本海默近似下，體系波函式可以被寫為電子波函式與原子核波函式的乘積
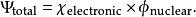從頭計算法玻恩－奧本海默近似由於在大多數情況下非常精確，又極大地降低了量子力學處理的難度，被廣泛套用於分子結構研究、凝聚體物理學、量子化學、化學反應動力學等領域。
玻恩–奧本海默近似是由物理學家奧本海默與其導師玻恩共同提出的。
利用玻恩－奧本海默求解薛定鍔方程的步驟
首先將體系的哈密頓算符分解為原子核動能算符與電子哈密頓算符兩項
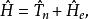從頭計算法其中電子哈密頓算符包含所有靜電相互作用(電子－電子，電子－核及核－核相互作用)，以及電子的動能算符。
接下來，解以下的電子薛丁格方程以獲得電子波函式和絕熱勢能面：
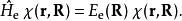從頭計算法這一步一般被稱為電子結構計算，由於電子的數量往往遠大於原子核，這一步往往是整個計算最昂貴的一步。根據計算能力，體系複雜程度和精度的需要，可以採用各種從頭計算法直接近似求解，也可以採用密度泛函理論，半經驗方法，分子力學勢場等一系列方法獲得勢能面。
獲得勢能面之後，可以用其求解原子核的定態薛丁格方程得到原子核波的定態函式和體系能量
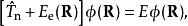從頭計算法或通過求解含時薛丁格方程模擬原子核波函式隨時間的演化
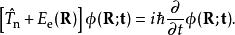從頭計算法這兩種方法獲得的結果可以互相轉化。原子核定態波函式描述了分子的振動，一般用來獲得振動零振動點能，進行紅外、微波光譜或電子光譜振動與轉動結構的計算；而波函式隨時間的演變則描述了化學反應的動力學過程。
注意到第二步原子核薛丁格方程的求解中，需要電子態能量以原子核位置為坐標的函式，因而往往需進行多次，乃至數千萬次電子結構的計算，造成計算嚴重的困難。即使在小分子體系中，往往也無法採用完全量子理學的方法求解波函式。由於原子核的質量比電子大得多，量子效應不如電子明顯，因此這一步往往採用比電子結構步驟更高程度的近似方法，以減輕計算負擔。例如常採用經典力學或者半經典近似處理原子核運動；在振動幅度較小的情況下，可將勢能面近似為二次曲面，而原子核的運動則轉化為量子諧振子問題而可解析解出。某些情況下亦可採用平衡態的近似，運用統計力學或過渡態理論等統計方法則，只需要在少量關鍵位置進行電子結構和振動計算就得到關於分子的分布或反應速率等信息。
適用性
玻恩-奧本海默近似只有在所在電子態與其他電子態能量都足夠分離的情況下才有效。當電子態出現交叉或者接近時，玻恩－奧本海默近似即失效。
最低值原理
對於基態，不加其他近似的情況下通過玻恩－奧本海默近似得出的體系總能量一定小於體系真實能量，因而給出了真實能量的下限。與此相對，另一絕熱近似方法玻恩－黃近似則給出體系真實能量的上限。
哈特里－福克方程
哈特里－福克方程（英語：Hartree–Fock equation），又稱為 HF方程，是一個套用變分法計算多電子系統波函式的方程，是量子物理、凝聚態物理學、量子化學中最重要的方程之一。HF方程形式上是單電子本徵方程，求得的本徵態是單電子波函式，即分子軌道。以HF方程為核心的數值計算方法稱為“哈特里－福克方法”（Hartree–Fock method）。
基於分子軌道理論的所有量子化學計算方法都是以HF方法為基礎的。鑒於分子軌道理論在現代量子化學中的廣泛套用，HF方程被視為現代量子化學的基石。
哈特里-福克近似
哈特里-福克近似也稱為 分子軌道近似或 單行列式近似，認為多電子體系波函式可以由體系分子軌道波函式構造的單個斯萊特行列式表示：
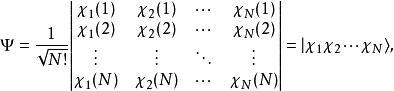從頭計算法
從頭計算法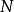
從頭計算法 從頭計算法這裡 為電子數， 是能量最低的 個分子軌道波函式。而分子軌道波函式是由體系中所有原子軌道波函式經過線性組合構成的，
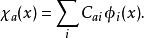從頭計算法
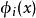從頭計算法通常原子軌道波函式 由計算時指定的基組給出。
在此近似下，由變分法，體系的多電子薛丁格方程可化為單電子方程
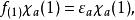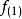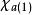從頭計算法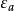
從頭計算法
從頭計算法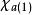
從頭計算法 從頭計算法其中 為福克算符， 為體系的分子軌道， 是分子軌道 的軌道能。這就是 哈特里-福克方程。求解該方程，即求解使方程成立的一組分子軌道；這組分子軌道使得在HF近似下的體系總能量最低。
發展簡史
1927年，物理學家沃特·海特勒和弗里茨·倫敦完成了氫氣分子的量子力學計算之後，開啟了量子化學的時代。從此，人們便開始嘗試使用量子力學理論來解釋化學物質結構和化學現象。
為了解決多電子體系薛丁格方程近似求解的問題，量子化學家道格拉斯·哈特里在1928年提出了哈特里假設，將每個電子看做是在其他所有電子構成的平均勢場中運動的粒子，並且首先提出了疊代法的思路。哈特里根據他的假設，將體系電子哈密頓運算元分解為若干個單電子哈密頓運算元的簡單代數和，每個單電子哈密頓運算元中只包含一個電子的坐標，因而體系多電子波函式可以表示為單電子波函式的簡單乘積，這就是 哈特里方程。但是由於哈特里沒有考慮電子波函式的反對稱要求，他的哈特里方程實際上是非常不成功的。
1930年，哈特里的學生弗拉基米爾·福克和約翰·斯萊特分別提出了考慮泡利原理的自洽場疊代方程和單行列式型多電子體系波函式，這就是 哈特里-福克方程。但是由於計算上的困難，HF方程誕生後整整沉寂了二十年，在1950年，量子化學家克萊門斯·羅特漢想到將分子軌道用原子軌道的線性組合來近似展開，而得到了閉殼層結構的羅特漢方程。
1953年，美國的R.帕里瑟、R.帕爾和英國的約翰·波普爾花費兩年時間使用手搖計算器分別獨立地實現了對氮氣分子的RHF自洽場計算，這是人類首次通過求解HF方程獲得對化學結構的量子力學解釋，也是量子化學計算方法第一次實際完成。在第一次成功之後，伴隨著電腦技術的迅猛發展，HF方程與量子化學一道獲得長足發展，在HF方程的基礎上，人們發展出了高級量子化學計算方法，使得計算精度進一步提高，通過對HF方程電子積分的簡化和參數化，人們大大縮減了量子化學的計算量，使得對超過1000個原子的中等大小分子的計算成為可能。
相關條目
•非絕熱耦合
•薛丁格方程
•玻恩－黃近似
•玻恩定則
